Whistler Alley Mathematics
These are some mathematics investigations I have pursued over
the years. They may be of some interest to teachers, students, or hobbyists.
I try to convey a conceptual understanding, usually without rigorous proof.
Some of the lessons are accompanied by questions and suggestions for extensions.
In my pursuit of a teaching career, I was told to justify the
study of each concept by establishing its relevance to the students’ lives.
Sorry, but I still have trouble buying into that one. Fortunately, poetry
and music are rarely put to that same test. As I glance at the list below,
I must concede that it would be difficult to convert any of the lessons
into food, shelter, or money. These are things that interested me, and
now I understand them better. If there is a reward, it is the fact that
every time I do this I get better at figuring things out.
I occasionally get email from people seeking permission to use my work. Feel free to cite, quote, edit,
reproduce, or distribute anything on this site. Do not worry about putting my name on it,
but please do not put your own name on it.
Many of these presentations use the Geometer’s Sketchpad, but only one of them actually requires it. If you do not have the software, let me suggest that you follow this link to Key Curriculum Press and look into it.
Paul Kunkel
Recent Changes
|
February 18, 2020 |
Updated the Conics_Plus tools, available in The Geometer's Sketchpad Workshop.
|
|
March 16, 2016 |
Updated the animations on Hanging With Galileo.
|
|
October 23, 2015 |
Updated the animations on Reuleaux Triangle.
|
|
October 9, 2015 |
Updated the animations on the Vernier Scale page of the Geometry of Surveying.
|
|
October 8, 2015 |
Updated the animations on Linkages.
|
|
October 4, 2015 |
Updated the animations on On the Square.
|
|
September 25, 2015 |
Updated the animations on Tangent Circles.
|
|
September 23, 2015 |
Updated the lead page of Conic Sections and Construction.
The page it replaced had java animations that were not being treated well by modern browsers. New images were generated with the developmental Web Sketchpad, which is producing very satisfying results. This appears to be the future, so expect more of my pages to be similarly updated soon. |
|
 Includes GSP-3 files Includes GSP-3 files
|
 Includes GSP-4 files Includes GSP-4 files
|
 Includes GSP-5 files Includes GSP-5 files
|
Contents:
|
We are given two fixed points in a vertical plane. A particle starts from rest at one of the points and travels to the other under its own weight. Find the path that the particle must follow in order to reach its destination in the briefest time.
This is a famous problem in the calculus of variations. Nothing new is presented here, but the explanation is more thorough than most.
|

|

An old probability exercise is aided by an interactive Sketchpad file.
By manipulating the sketch, an intuitive understanding may be gained, even
if the student has had no introduction to calculus.
|
This has no lesson, only questions. It is just an interesting animated
file, which invites student investigation. It has applications for geometry,
trigonometry, and probability. Fair warning: The discussion revolves about
a figure that appears only when the sketch is animated. Without Geometer’s
Sketchpad, this one will make little sense at all.
|

|
|
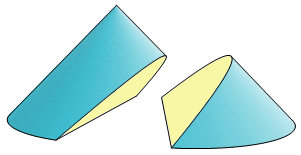
My emphasis is on geometric properties of the conic sections, particulary understanding that has been handed down to us in ancient texts. There also are some challenging constructions. |
|
|
This used to be my job, and I enjoyed studying all of the geometrical concepts that were part of the science of land surveying. In this article I discuss the instruments of the profession, their operating principles, their error, and their calibration. |
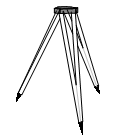
|

An investigation into the catenary, the curve formed by a chain suspended
at both ends. It also extends into the curve of the main cables on a suspension
bridge, which, interestingly, is not a catenary.
|
If you have never studied inversion geometry, you can start here. The elementary concepts are explained. This page is a quick reference for the other lessons that employ inversion geometry.
|
|
|
Draw a line segment. Did you use a straightedge? How do you know it was
straight?
Java simulations are used to investigate a nineteenth century mechanics
problem. |
|
|
The challenge: Given four arbitrary, unique points, A, B,
C, and D, construct one line through each point such that the four lines form a square. |
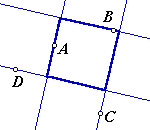
|
|
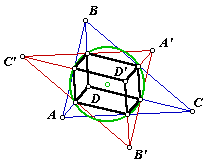
What is so significant about the orthocenter of a triangle? Why does it
even have a name? This investigation was prepared for a geometry teachers’
workshop. It includes a lesson handout in Word format. This lesson was written for use in a computer lab with the Geometer’s Sketchpad, but with a little editing it should work just as well with Cabri or Cinderella. |
 |
|
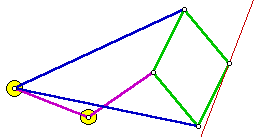
A planimeter is a drafting instrument used to measure area. Its mechanism
is quite simple, but understanding why it works is more elusive. |
 |
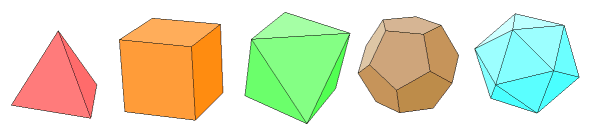
Find the inradius, circumradius, dihedral angle, surface area, and volume of all of the Platonic solids. There is also some information about some of their other interesting properties.
|
It is not a circle, but it has constant width. Study the properties of this figure
with interactive animated sketches. |
 |

How is that for a descriptive title? Here are investigations of two
interesting visual effects seen from a moving automobile. It includes two
interactive perspective drawings, and a discussion of the cylindrical and
planar projections used to create them.
|
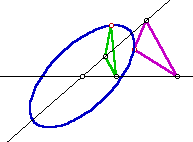
An interesting accidental discovery – Investigate ellipses
by tracing triangle transformations. |
|
|
Explore geometric patterns formed in a table of modular multiplication.
This one requires some elementary knowledge of congruence classes and modular
arithmetic. |
|
|
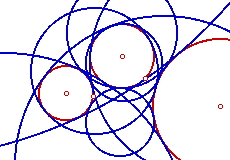
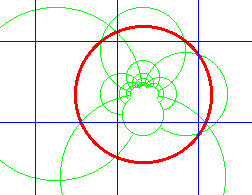
Three circles are given. How many circles can be constructed tangent
to all three? How are they constructed? This lesson includes ten animations covering all of the special cases. Some of them are very complex. A little knowledge of circle inversions would help. |
|
|
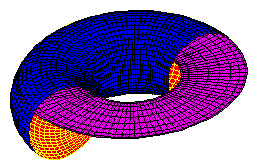
Do you already know the volume of a torus? Then humor me. I just figured
it out, and I got a chance to try out this new graphics software. |
|
Resources
|
It is plain to see that I am very fond of Sketchpad. This page was created after the release of version 4. The idea is to have a place to exchange ideas with other users, especially those who are using the advanced features. Here are some custom tools and some information on Java Sketchpad.
|

|
|
These are some of my best sketches. You may find them useful or interesting
by themselves. |

|
|
Thirteen elementary straightedge
and compass constructions are described and illustrated. The original version,
in Word format, can be downloaded and distributed. |
|
Back to Whistler Alley
Last update: February 18, 2020 ... Paul Kunkel whistling@whistleralley.com
For email to reach me, the word geometry must appear in the body of the message.
|