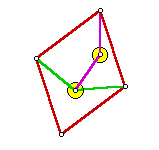
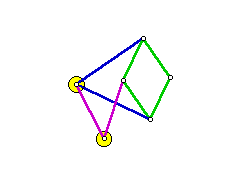
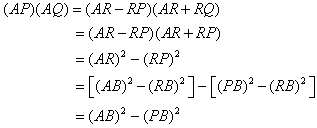Linkages

This lesson has several references to inversion geometry. If you are unfamiliar with the subject, you may wish to refer to this guide: Inversion Geometry

This is a geometry challenge that might seem to be simplistic: We want a mechanism that will draw a straight line segment. Your first impulse is to draw it with a straightedge, but that would not be fair. Somebody else had to make the straightedge straight. When you think about it, circles are easy. A compass can be made from any rigid object. Attach a pin to one end of a canoe paddle, and attach a pencil to the other. The paddle will draw a perfect circle. But using a straightedge requires a leap of faith. We cannot be certain that it is straight.

In 1864, the problem was solved by Captain Charles-Nicolas Peucellier, a French artillery officer. Several other linkages followed. Some were simpler, but they all seem to be variations of the Peucellier linkage. In 1877, they were summarized in How to Draw a Straight Line: A Lecture on Linkages, by Alfred Bray Kempe. The book was reprinted by the National Council of Teachers of Mathematics in 1977. All of the linkages presented here are from that book.

Peucellier approached the problem with inversion geometry. He knew that the inverse of a circle through the center of inversion is a line. It is easy enough to make a point follow a circle, so he only needed to design a linkage that would invert that point. The image below is called the Peucellier cell. All of the line segments represent rigid links, like colors are congruent, and the intersection points are hinges. It will be shown that if point A is fixed and point P moves freely (as far as the links will allow it), then point Q is the inverse of point P. The center of inversion is A. The power of inversion, r², will be derived in the proof.

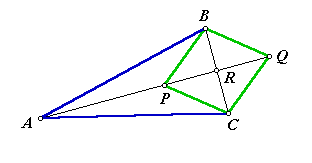
For the purpose of this proof, let it be given that AB > PB. That is to say that the blue links are longer than the green links. It must be shown that if P moves while A is fixed, the product (AP)(AQ) is equal to some constant r². It is clear from the symmetry that points A, P, and Q are collinear. Let point R be the intersection of the diagonals of quadrilateral PBQC. Since it is a rhombus, the diagonals must be perpendicular.

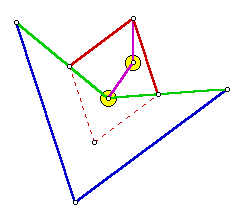
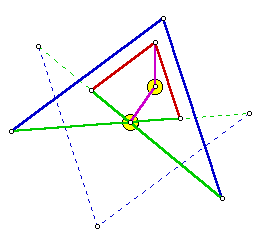
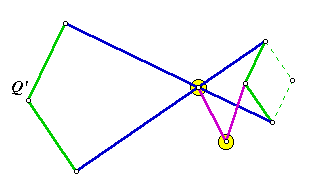
The values AB and PB are measures of rigid links, and therefore are constant. This means that the product (AP)(AQ) is constant. Let r² =  AB)² - (PB)². Do you see now why we needed the condition AB > PB? Actually, the linkage will still work, even if the green links are longer than the blue. The linkage would work, but the proof would not. In that case, points P and Q would not be inverses of each other. There would be another transformation between them. See if you can work it out.

The only thing left is to force point P into the path of a circle through A. The linkage below should do the job. The small circles represent fixed anchor points. Since they are fixed, the link between them is unnecessary, but it is there to show the geometric relationship. Notice that point labelled drag (corresponding to P) cannot trace the entire circle without breaking some of the links. Hence, the trace is a line segment rather that an entire line. Drag the point to see a simulation.

Other Working Linkages

Below are some other linkages that draw straight line segments. It will be seen that they are actually variations on the Peucellier linkage.

It may look different, but this is the Peucellier linkage again. Geometrically, there is no reason why the rhombus links should have to be shorter than the others.
Using the lower anchor as the dilation point, dilate the lower part of the cell. That point at the bottom is the new pencil point. The locus of its pre-image was a line segment, so this point must trace the dilation of that line segment, which is simply another line segment.
Try another dilation. This time use a dilation ratio of -1. That causes the new pencil point to be on the other side of the anchor. Still it must trace a line segment.
Drag the point below to see another simulation.

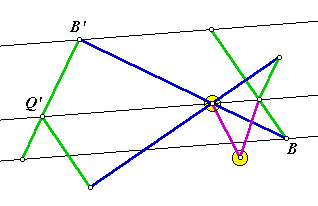
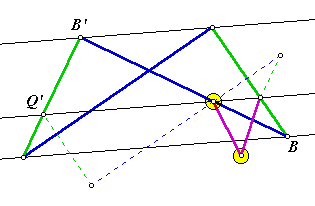
Fewer Links

This version is the simplest mechanism, but it may be more difficult to understand.

Once more, begin with the Peucellier linkage.
Dilate four of the links about the upper anchor point. Point Q' is the new pencil point. Since its pre-image traced a line segment, this point will too. The two links on the right may now be discarded without compromising the mechanism.
Draw the line of symmetry of the original cell, and draw parallel lines through points B and B'. Two of the links are extended to the two outside lines. Notice that these two links intersect the parallel lines at the same angle, and are therefore congruent. In fact, they are the legs of an isosceles trapezoid with diagonal BB'. Point Q' is still the pencil point.
Insert another link as the other diagonal of the trapezoid. This will support the shape of the mechanism, so some of the other links now may be removed.

Of all of the solutions, this appears to be the most economical. Drag the point to view a simulation.

Web Sketchpad Files

The animated sketches on this page were created with Web Sketchpad, a developmental version of The Geometer’s Sketchpad.