The Sliding Triangle

If you read the Reuleaux Triangle lesson, you may have wondered about the curves traced by the centroid and vertices of the Reuleaux as it rotated within the rhombus. Essentially, what we had was a rigid figure with two of its points sliding along intersecting lines. I want to examine the locus of a third point on the figure.

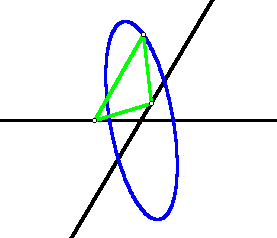It was easy enough to model the configuration on Sketchpad. Since we are interested in only three points of the figure, substitute a triangle and have two of the vertices attached to intersecting lines. When I move the triangle along the lines, the trace of the third vertex appears to be an ellipse, but that has not been proved.

To understand this problem, it might be helpful to review the definitions of the ellipse. It has several equivalent definitions:

An ellipse is a conic section, the intersection of a right circular cone and a plane which is parallel to none of its generators.

An ellipse is the set of all points in the plane, whose undirected distances from a fixed focus are in constant ratio e to their distances from a fixed line (directrix), where 0 < e < 1. The parameter e is called the eccentricity.

An ellipse is the locus of all points in the plane, the sum of whose distances from two fixed foci is constant.

An ellipse in standard position, with semi-major axis a and semi-minor axis b, may be defined as the set of all points satisfying this equation:

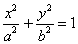
That same ellipse may be defined by these parametric equations:

x = acosθ, y = bsinθ

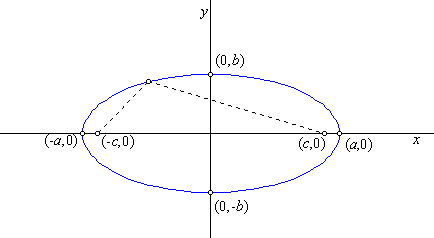
That last definition, with the parametric equations, is the one I want to use. Here is a corresponding sketch. The coordinates of the foci use the constant c, defined by this equation: c² = a² - b². It may also be defined in terms of the eccentricity, e. c = ae.

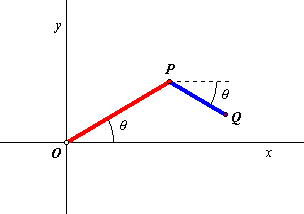Now click this image to open a Java applet. You will see the construction shown in this sketch. Drag point P in a circle around the origin and watch the trace of point Q. The red segment has length (a + b)/2. The length of the blue segment is (a - b)/2. Using this information, you should be able to compute the coordinates of point Q in terms of θ. Do this and verify that its coordinates match those of the parametric equation for an ellipse. Try changing the lengths of the segments, and see how it affects the ellipse.

Notice that the directions of OP and PQ change at the same rate, but in opposite rotation directions. Also notice that the lengths of the segments do not matter. That is, we never did say what a and b were. We can choose arbitrary segment lengths and use them to define a and b. From this we can make a general statement. Given a point P tracing a circle about some fixed center O, if point Q revolves about P at the same rate, but opposite direction, and if OP and PQ have constant lengths, then Q must trace an ellipse.

I skipped a few steps there, so maybe you can fill in the gaps. Since OP and PQ are rotating in opposite directions, they must be parallel for some orientation, but not necessarily on the x and y axes, as in the example above. In fact, there is no reason that O has to be the origin. If you start with any points O, P, and Q, you should be able to just set them in motion. Point P orbits O, and Q orbits P, like a star, a planet, and a moon. If they have the same orbital period, but opposite direction, then point Q will trace an ellipse. Try it.

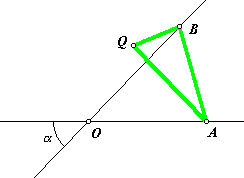So how does this fit in with the triangle that is tethered to the two intersecting lines? Click this image to open another applet. Play around with it first. See how the ellipse changes as you change intersection angle α, or as you change the shape of the triangle. What happens when you form an isosceles triangle? How can you make it trace a circle? Or a line segment?

In this applet, triangle ABQ may move freely as long as points A and B stay on their respective lines, which are fixed with angle α. Do you see any points traveling in a circular path? Neither do I. But try looking at it another way. We can construct a circle through points A, B, and O. Label the center P. While the circle moves, the inscribed angle BOA is constant, α. Therefore, the interior angle BPA is constant, 2α. That interior angle subtends a constant chord, AB, therefore the circle has constant radius.

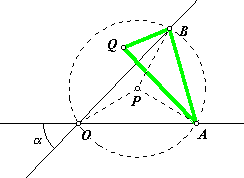You should be able to see several important relationships in this picture. Distance OP is constant, so P travels in a circle about O. PA and PB are constant, so that fixes P with respect to segment AB, and hence, with respect to the triangle. Therefore, PQ has constant length. If it can be shown that OP and PQ rotate in opposite directions at the same rate, then that will show that Q traces an ellipse. That part is left as an exercise.

Here are some other things to think about. Many of the answers may be found (without explanation) by showing the hidden work in the Sketchpad file below.

What are the angles PAB and PBA?

How can you construct the parameters a, b, and c?

What about the orientations of the semi-major and semi-minor axes?

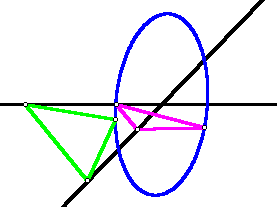I discovered that each of these triangles has what I call a ghost, a different triangle which may be attached to the same pair of lines to generate the same ellipse. Do you see how the ghost is constructed? Hint: in the first applet, see what happens when you use the same segment lengths but in a different order.

Since this all started with the Reuleaux triangle, maybe we should bring it back to that. In the section where I wrote about the trace of the centroid, I said that it did not trace an ellipse. That was correct. As the reuleaux triangle rotates in a rhombus, the centroid follows four distinct curves. Each is a part of an ellipse. The changes occur because the vertices slide on different sides of the rhombus. If the acute angle of the rhombus is lest than 60°, then two of the curves will be circular arcs.

Geometer’s Sketchpad Files

The Java applets presented here were created with the Geometer’s Sketchpad. The corresponding Sketchpad files may be downloaded here.

Back to Whistler Alley Mathematics