The BrachistochroneThe brachistochrone problem is a seventeenth century exercise in the calculus of variations. In his solution to the problem, Jean Bernoulli employed a very clever analogy to prove that the path is a cycloid. Much in the way that Archimedes applied laws of gravitation and leverage to purely theoretical geometric objects, Bernoulli solved a gravitation problem through the use of seemingly unrelated properties of light refraction. This presentation is based on his solution. The brachistochrone challenge: We are given two fixed points in a vertical plane. A particle starts from rest at one of the points and travels to the other under its own weight. Find the path that the particle must follow in order to reach its destination in the briefest time. Just to get some ground rules straight, this problem is set in one of those perfect worlds that exist in the minds of theorists. In this world, gravitational acceleration is constant in both direction and magnitude. The particle is a point, but has mass, and hence, weight. Being a point, it is not burdened with moment of inertia or friction. However, it somehow can be forced to follow a path without gaining or losing energy. Anyone wishing to throw special relativity into the mix is advised to browse to some other website. BrainstormIt is my hope to make this subject at least partially accessible even to students who have never studied calculus. For that reason, this section is a discussion of some of the thought processes that might go along with such a problem. If you would prefer to do this analysis on your own or not at all, you will not hurt my feelings by skipping down to the solution. One physical law that must be observed is that the speed of a falling object is a function of its height. Slides, swings, or anything else that is introduced may alter the particle's course, but its speed at any given height will be the same no matter what its direction of travel or what path it took to get to that level. The lower it is, the faster it travels. Since the particle starts from rest, it cannot rise any higher than its beginning elevation. That would be like falling up a hill.
What if it does travel on a rectangular path? There is any number of rectangular paths between two points. In both of these images, the particle travels down, then right, then up. In the second image, it falls further down than it did in the first, so it must travel a greater distance. On the other hand, the horizontal trip across is faster in the second. If it does take a rectangular path, how far should it fall?
The answer to that question might make an interesting extension, but, in fact, there are many reasons not to take a rectangular path at all. The first reason is physical. A rectangular path would require a moving object to undergo an instantaneous change in direction, which is physically impossible. Since the particle has mass, it would require an infinite amount of energy. The only way for the particle to follow that path would be to slow to a stop at the angle point, then accelerate in the other direction. This would require us to store and release energy, just as a pogo stick does. If that were the case, the particle would be propelled by a force other than its own weight. The rules do not seem to allow that, but it is a moot point. It can be shown that the quickest path is a smooth curve. It has no angle points.
In that last inequality, t is the travel time along the red segment and through the angle, and t' is the time taken by the shortcut. It would appear that angles are a waste of time. 
It was explained that if the endpoints of the path have the same elevation, then the path will have to descend from the start and come back up to the finish. So, there is at least one case in which the curve would go down and then back up. It can be proved that there is no case in which any part of the quickest path goes up and then back down. More generally, show that no part of the curve is concave downward. That proof is left to the reader. Before proceeding to the solution, let us summarize the conclusions:
The SolutionLet the starting point from which the particle is released be the origin
In this equation, v is the speed of the particle and g is the acceleration of gravity. Keep in mind that the particle is being release from the origin. The y-coordinate cannot be positive, because a falling object cannot reach a level higher than its point of release. Of course, if the finishing point is higher than the starting point, there is no solution. Imagine the particle falling through a stack of planes. At each plane, it has a different speed.
Snell’s Law: n1sinθ1 = n2sinθ2 where ni = c/vi (the index of refraction in medium i); c is the speed of light in a vacuum, and vi is the speed of light in medium i. The connection between Fermat’s Principle and Snell’s Law is explained here: Fermat
It may appear that by appealing to the physical properties of light, a mathematical derivation is being supplanted with some lowly Working from Snell’s Law, we can get some notion of the slope of the curve.
The constants a and g are both positive. This is the square of the derivative. It is undefined for y ≥ 0, and for y < -a2/(2g). Now, we look at the cycloid. A cycloid is usually pictured as the path of a point on a circle that is rolling along the ground like a wheel. This time, it is rolling on the ceiling, the x-axis. It starts at
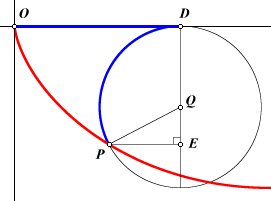
For comparison, we would like to find the square of the derivative of a cycloid. Let P be the point on the rolling circle that is tracing the cycloid. Let r be the radius of the circle, Q the center, and D the point of tangency between the circle and the x-axis. The x-coordinate of P can be expressed as
In this way, x has been expressed entirely in terms of the circle. Now zoom in on point P and look at the changes that occur when P is advanced an arbitrarily short distance along the circle to point G. The length of 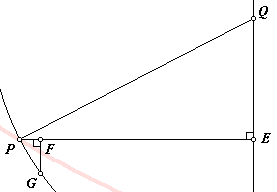
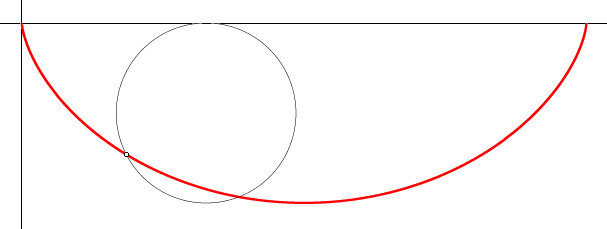
If we let r equal a2/(4g), then we find that this is the same as the square of the derivative of the brachistochrone, as derived above. This seems to lead us toward the cycloid as a solution. There are still some loose ends, but a cycloid is the solution. Let point O be the start again, and let point N be the finish. Draw an arbitrary cycloid beginning at O. Find the intersection, M, of line ON and the cycloid. Dilate the cycloid on O, using scale factor ON/OM.
Loose EndsI am not going to do all of the clean-up work, but I will point out some remaining problems and leave them as exercises, beginning with the hardest one. This part is a bit disconcerting. I have seen several explanations of the brachistochrone in textbooks and on the Web. Undoubtedly, this issue has been addressed before, but I have not seen it. All of the treatments I have read arrive at some form of this differential equation:
Then, in one way or another, they prove that there is a cycloid that satisfies the equation, and leave it at that. Is the cycloid the only solution? In fact, it is not. The brachistochrone is a cycloid, but that cycloid is not the only curve satisfying the equation. The equation shows the form of the square of the derivative. We can get the magnitude of the derivative from this, but not its sign. Where does it go up, and where does it go down? Must it match the cycloid? Both the brachistochrone and the cycloid start out downward. Neither curve can have a discontinuous derivative (which is what that angle point discussion was all about), so neither curve can slope upward until after the derivative has first reached zero. If they part ways, it will have to be at the point where they level off. The brachistochrone cannot go down from there, because its derivative would be undefined, and also it would have downward concavity. But who says it cannot continue horizontally for a while before it turns upward? That path would not conflict with the equation.
(1) Prove that the cycloid is the quickest path in the family. Hint: Of the curves in this family, the cycloid is the only one that does not include a horizontal line segment. Consider a horizontal line segment below the x-axis, then prove that there must be a quicker path between the endpoints of the line segment. (2) Prove that there are no solutions to the differential equation and initial conditions outside of this family of curves. (3) What is so special about the line (4) The square of the derivative of the cycloid could have been derived analytically, but it was done geometrically. That was in keeping with the geometry theme of this site, but mostly it was because I like to draw pictures. A sharp reader may have noticed that the calculations depend on point P being below and left of point Q. In any other position, some of the signs will change, but the end result will be the same. Prove that this is so. (5) Consider the special case in which point N is on the (6) Go back to Bernoulli’s theoretical model of a medium with a continuously variable density, causing light to travel at the same speed as falling objects. If a laser were pointed vertically downward through this medium, would the beam follow a cycloidal path? If not, is this a contradiction? Back to Whistler Alley Mathematics
|
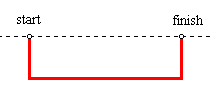 Before getting into the figures, consider a few possibilities. Even among mathphobes there is a common expression stating that the shortest distance between two points is along a straight line. It is the shortest path, but is it also the quickest? This path can be easily dismissed with a counterexample. If the beginning and end points are at the same elevation, then the line between them is horizontal. The weight of the particle cannot cause it to slide on level ground. It must first drop below the starting elevation in order to get some headway. A rectangular path would get it to the destination, though not necessarily in the briefest time. So, the direct path is not the quickest, at least not in all cases.
Before getting into the figures, consider a few possibilities. Even among mathphobes there is a common expression stating that the shortest distance between two points is along a straight line. It is the shortest path, but is it also the quickest? This path can be easily dismissed with a counterexample. If the beginning and end points are at the same elevation, then the line between them is horizontal. The weight of the particle cannot cause it to slide on level ground. It must first drop below the starting elevation in order to get some headway. A rectangular path would get it to the destination, though not necessarily in the briefest time. So, the direct path is not the quickest, at least not in all cases.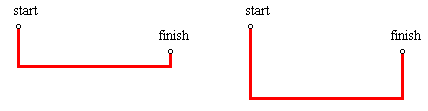
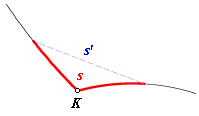 This was supposed to be taking place in one of those special worlds. Suppose that in this world, instantaneous change in velocity is possible. In this example, the path follows a curve to an angle point, K, then abruptly turns onto another curve without losing any speed. The angle of intersection is the angle formed by the tangents back and ahead. It will be shown that there is always a quicker shortcut across the corner. Let s be the length of a small segment of the path (highlighted in red) starting a short distance ahead of point K and continuing the same distance beyond it, and let v be the average speed of the particle along s. Let s' be the length of the line segment connecting the endpoints, and let v' be the average speed along that line segment. Clearly, s must be greater than s'. As we zoom in and use a smaller value for s, the segment and the shortcut approach the shape of an isosceles triangle. The average speeds, v and v' both approach the speed at point K. Since they approach the same constant, the ratio v'/v approaches 1. The ratio s'/s approaches some constant that is less than 1.
This was supposed to be taking place in one of those special worlds. Suppose that in this world, instantaneous change in velocity is possible. In this example, the path follows a curve to an angle point, K, then abruptly turns onto another curve without losing any speed. The angle of intersection is the angle formed by the tangents back and ahead. It will be shown that there is always a quicker shortcut across the corner. Let s be the length of a small segment of the path (highlighted in red) starting a short distance ahead of point K and continuing the same distance beyond it, and let v be the average speed of the particle along s. Let s' be the length of the line segment connecting the endpoints, and let v' be the average speed along that line segment. Clearly, s must be greater than s'. As we zoom in and use a smaller value for s, the segment and the shortcut approach the shape of an isosceles triangle. The average speeds, v and v' both approach the speed at point K. Since they approach the same constant, the ratio v'/v approaches 1. The ratio s'/s approaches some constant that is less than 1.
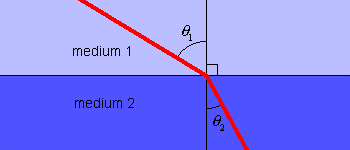 Bernoulli found an equivalent way of viewing it. Instead of a particle subject to the force of gravity, he considered a light ray traveling through different media. The speed of light depends on the medium through which it travels. When it crosses a boundary from one medium to another, it is refracted. Fermat’s Principle states that as light travels across a boundary from one point to another, it takes the quickest route, which generally is not the most direct route. It stands to reason that the solution to the brachistochrone might be derived by imitating the behavior of light. Light always finds the quickest path because it follows Snell’s Law of Refraction.
Bernoulli found an equivalent way of viewing it. Instead of a particle subject to the force of gravity, he considered a light ray traveling through different media. The speed of light depends on the medium through which it travels. When it crosses a boundary from one medium to another, it is refracted. Fermat’s Principle states that as light travels across a boundary from one point to another, it takes the quickest route, which generally is not the most direct route. It stands to reason that the solution to the brachistochrone might be derived by imitating the behavior of light. Light always finds the quickest path because it follows Snell’s Law of Refraction.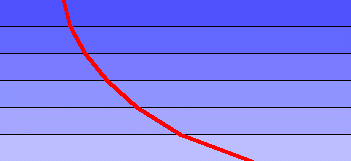 Now, imagine a light ray traveling downward through many layers of diminishing density. Through any given layer, let the density of the medium be such that the speed of light is the same as the speed of a falling object at the height of the middle of the layer. As the thickness of the layers is diminished, the path of the light approaches a differentiable curve, and the speed of the light may be described by the same equation used above:
Now, imagine a light ray traveling downward through many layers of diminishing density. Through any given layer, let the density of the medium be such that the speed of light is the same as the speed of a falling object at the height of the middle of the layer. As the thickness of the layers is diminished, the path of the light approaches a differentiable curve, and the speed of the light may be described by the same equation used above: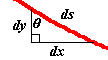 This means that, at every level, the ratio of the velocity to the sine of the angle of incidence is equal to the same positive constant, a. The exception is the starting (and perhaps the finishing) point, which is on the x-axis, where the velocity is zero and there is no angle of incidence. In this image, an arbitrarily small segment of the curve is shown. As its length diminishes, the three sides of the figure approach a right triangle. Some useful relations can be seen.
This means that, at every level, the ratio of the velocity to the sine of the angle of incidence is equal to the same positive constant, a. The exception is the starting (and perhaps the finishing) point, which is on the x-axis, where the velocity is zero and there is no angle of incidence. In this image, an arbitrarily small segment of the curve is shown. As its length diminishes, the three sides of the figure approach a right triangle. Some useful relations can be seen.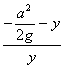
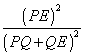
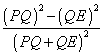
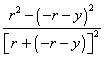
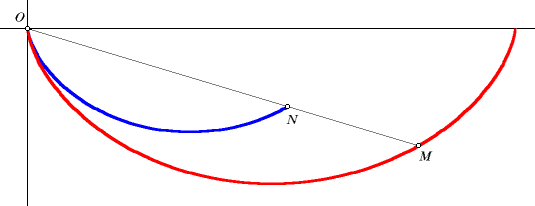
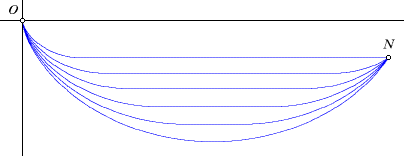 If point N is above the line
If point N is above the line