
The study of polyhedra makes for a great workout. There are many manipulative models available to facilitate this. With practice, a strong spatial sense can be developed. It becomes possible to mentally lift a figure and rotate it, dissect it, peel it, and reassemble the pieces into something else. Work on polyhedron properties long enough and many cumbersome symbolic operations will become second nature. Formulas, identities, and algorithms start to spill out onto the page without a thought.
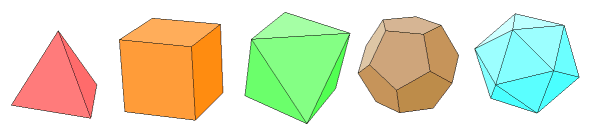
The Platonic solids are a special set of polyhedra. What distinguishes them is that all of their faces are congruent regular polygons, with the same number of faces meeting at every vertex. This section will walk through some derivations for various attributes of the Platonic solids, including dihedral angle, inradius, surface area, and volume.
Below are some formulas that will be used in these investigations. Follow the link to see the formula derivations.
Begin with the following variable definitions:
s = side length of a regular polygon or edge length of a Platonic solid
n = number of sides on each face
f = number of faces on a Platonic solid
|
|
The apothem of a regular polygon is the distance from center to the midpoint of a side. It is also the radius of the inscribed circle. Only regular polygons have an apothem. |
|
|
|
for regular polygons only |
|
|
|
for Platonic solids only |
|
|
|
This formula applies only in the case in which exactly three faces meet at a common vertex. Other cases will be addressed as they arise. This is the angle of intersection of faces having vertex angles α and β. The vertex angle of the third face is γ. |
The inradius is the radius of the sphere inscribed in a given polyhedron. The circumradius is the radius of the circumscribed sphere. All Platonic solids have an inscribed sphere tangent to every face and a circumscribed sphere through every vertex. Other polyhedra generally do not. These last three formulas apply only to Platonic solids.
|
|
|
|
|
|
|
|
The table below presents the inradius, circumradius, dihedral angle, surface area, and volume for each of the Platonic solids. Click on the name of the solid for more information about its properties and the derivations of the values that appear in this table.
|
solid |
inradius (ri) |
circumradius (rc) |
dihedral angle (θ) |
surface area (A) |
volume (V) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Users of the Geometer's Sketchpad may be interested in seeing the perspective renderings of the Platonic solids in this file:
Back to Whistler Alley Mathematics