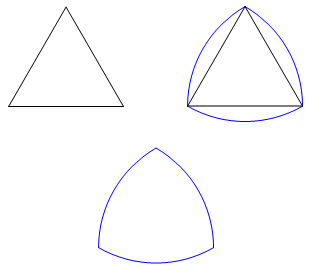
Reuleaux Triangle

I made some sketches of the reuleaux and discovered some other interesting properties. It can roll uphill, in a manner of speaking. If you have the ability to view Java, click on the Animate button at right to see a rolling reuleaux triangle. Notice that as it rolls, its height is constant, but the height of its centroid changes. If it had mass, the centroid would be the center of mass. Imagine that it is standing on one vertex, so that the centroid is at its highest, and imagine that the surface is very slightly inclined. If it moves forward one sixth turn, the centroid will fall. So although the surface rises, the reuleaux is actually falling.

The figure has constant width and constant height. It should be possible to inscribe one into a square and to turn it freely. Here is a sketch to simulate this. Animate the image. When I first saw it turning within the square, something looked very familiar about it. It looked a lot like those diagrams for the Wankel rotary engine. A Web search confirmed that this is the shape used for the rotor in the engine.

The square drill bit was not my idea either. Notice that as the reuleaux turns inside the square, its trace nearly fills the entire square. This shape can be used to drill square (actually squarish) holes, and in fact someone did manufacture a drill bit base on this concept. It is not just a simple matter of fitting a bit into a drill though. It required a more complex mechanism. As the reuleaux turns in the square, watch the motion of the centroid. For every rotation of the reuleaux, the centroid makes three revolutions in the opposite direction, and its path is not circular. Your next assignment is to design a mechanism that would make it work.

The reuleaux turns inside the square because the square is formed by two pairs of parallel lines equally spaced. Why should they have to intersect at right angles? Any rhombus has that same property. Collapse the square by dragging the point labeled tilt. It collapses into the shape of an oblique rhombus. It is still possible to inscribe a reuleaux and to rotate it. You will see some interesting contortions in the centroid locus as you change the rhombus.

A Few Questions:

As a reuleaux is inscribed between a pair of parallel lines and rotates between them, is there ever a time when no vertices touch the lines? One vertex? Two Vertices? All three vertices?

If a vertex of the reuleaux can touch a vertex of the rhombus, what can you say about the acute angle of the rhombus?

The shape of the centroid locus is not circular, but it is not a single ellipse either. It is composed of parts from four ellipses. To understand this better, see the Sliding Triangle page. Even without understanding the shape of the centroid locus, you should be able to prove that it has four symmetries. Can you prove this and can you define the symmetries?

To inscribe a reuleaux in a rhombus, it must touch every side, but cross none of them. Is it possible to inscribe and rotate a reuleaux in any polygon other than a rhombus?

The bumpy road that isn’t bumpy

I saved the toughest one for last. After seeing some of this work a friend handed me this challenge. See how the centroid of a reuleaux wheel rises and falls as it rolls an a level road. Is it possible to design a road profile that would result in the centroid following a level path? Below is a conceptual solution.

Here is how it works. At the point of contact, the wheel must be tangent to the road. The centroid must be directly above that point. That makes it fairly simple to derive the corresponding elevation of the road. The difficult part is finding the horizontal displacement of the centroid. Remember, the radius is effectively changing throughout, so that complicates things.

On the stationary wheel, a radial turns about the centroid. Next to that the radius is graphed with respect to the angle of rotation. Zero and the angle of rotation are the limits of integration for the area under the graph. This area is the horizontal displacement of the centroid. Note that the angle has no dimension, so the area under the graph actually has linear dimension. The results above are derived with a Simpson's approximation. I have not succeeded in deriving an exact expression for the curve.

Although the centroid follows a level path, this wheel still would not offer a very comfortable ride. Suppose that the wheel is propelling a vehicle (as opposed to being pulled along) and it is turning at a constant rotational rate. The changing radius would result in a changing velocity. The passengers would be constantly lurching forward and back.

Web Sketchpad Files

The animated sketches on this page were created with Web Sketchpad, a developmental version of The Geometer’s Sketchpad.