The Planimeter
The planimeter is a drafting instrument used to measure the area of
a graphically represented planar region. The region being measured may
have any irregular shape, making this instrument remarkably versatile.
In this age of CAD and digital images, I suspect that the planimeter is
heading toward obsolescence, but not just yet. They are still being manufactured.
When I first used a planimeter, I was somewhat troubled by the fact
that I did not understand how it worked. Oh sure, I don't understand how
my car works either, but the planimeter essentially has only three moving
parts. That makes its mechanism considerably less complex than a typical
doorknob. After eighteen years of sleepless nights, I decided to buy a
planimeter and figure it out.

This is my planimeter. I got it at a Snohomish antique mall.
It was made in Germany and distributed by Keuffel and Esser. The date on the bottom of the box says
1917. It is in perfect working condition, and it is nearly identical to
the instruments I was using in the early 80s. The brass cylinder is anchored
to the table with a point, like a compass point. It pivots, but does not
slide. The elbow joint bents and slides freely. The pointer on the other
end is used to trace the perimeter of the region. Near the elbow is a wheel,
which simply rolls and slides along the tabletop. The scale is on the wheel
itself, so it tells how far the wheel has turned. Sure enough, that number
is proportional to the area of the region. The conversion factor depends
on the scale of the drawing or photograph.
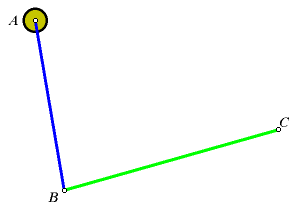
| Here is a schematic of the instrument.
If your browser supports Java, you can click on it and go to an interactive
sketch, allowing you to get the feel of it. Point A is stationary.
Point C traces the region in a clockwise direction. |
 |

The scale wheel is attached to the "green" arm, near point
B, and its axis is parallel to the green arm, BC. This orientation
is important. Suppose that the green arm has a translational motion. That
is, it slides but it is always pointed in the same direction. If it moves
longitudinally, then the wheel will not turn at all. It will merely slide
sideways. If the arm moves in any other direction, then the rotation of
the wheel will be proportional to the component of the translation that
is normal to BC. Also, it would not matter where the wheel is attached,
as long as it stays fixed to the green arm, with its axis parallel to BC.
You probably noticed that these conditional statements are not realistic.
The green arm most certainly does not always point the in the same direction.
It rotates as it moves. Just stay with me on this one. We are going to
start with some simple cases.
I have confirmed, mathematically and experimentally, that the length
of the blue arm, AB, is irrelevant. That length must be constant,
but the results will be the same no matter what the length is. Again,
humor me on this, at least for now. Point A is fixed, and AB
is some fixed distance, so the blue arm acts as a compass, and point B
travels along a circle. Since the distance AB does not matter, let
point A be sent a very long distance away. As A approaches
a point at infinity, the arc traced by point B approaches a line.
|
With this modification, we have
designed a different type of planimeter. This is not the same as the polar planimeter,
but it should work. The blue arm has been eliminated from the mechanism.
Point B slides along a straight groove. As before, point C
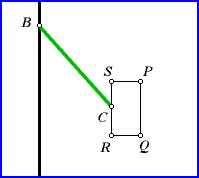
traces the region in a clockwise direction. Let's see what happens when we trace a very simple region, rectangle PQRS, two sides of which
are parallel to the path of point B. Start at point P and
move in a clockwise direction. Again, if you have Java, click on the sketch
to see a simulation.
Shortly after this web page was created, I found a planimeter that operates just this way. It is called an Amsler integrator. It is very large, and it was used primarily for measuring cross-section areas on boat plans.
|
|
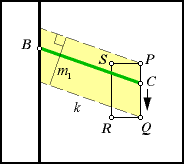
| As point C moves from P
to Q, point B must move the same direction and distance.
So the green arm moves without turning, just as we said. As it is translated,
the green arm sweeps across the yellow parallelogram shown in this illustration.
Let m1 be the measurement read by the wheel as C
goes from P to Q. Since the wheel measures only the normal
component of the translation, m1 must be the height of
the parallelogram. Let k be the length of the green arm: k = BC
This is also the base of the parallelogram, so the area of the yellow parallelogram
is km1. |
|
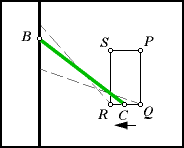
| Look what happens when we move
the pointer from Q to R. This time it is not a translation.
The green arm turns as it moves, so it is not so simple to tell what effect
it has on the measuring wheel. Just call that measurement m2,
and set it aside for now.
|
|
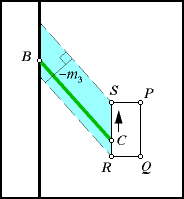
| Now go from R to S.
Once again, the green arm is translated. It sweeps across the blue parallelogram.
Let m3 be the wheel measurement taken over this interval.
Notice that, this time, the wheel is moving backwards, meaning that m3
must be negative. The height of the blue parallelogram is -m3.
Its area is -km3. |
|
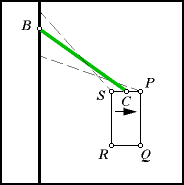
| Finally, we complete the circuit,
going from S to P. The green arm will turn this time. Call
the measurement m4. As with m2, it
is not easy to tell what the magnitude of m4 is. But
look again, and notice the symmetry. Going from S to P, the
motion of the arm is similar to the motion made when going from Q
to R. The only difference is that the motion is made in opposite
directions. Therefore, m2 and m4 must
be opposites: m2 = -m4
|
|
Let M be the final reading on the wheel, so M must be
the sum of the measurements made on the four sides.
M = m1 + m2 +
m3 + m4
M = m1 + (-m4) +
m3 + m4
M = m1 + m3
Multiply that measurement by k, the length
of the green arm.
kM = k(m1 + m3)
kM = km1 + km3
kM = km1 - (-km3)
kM = [yellow area] - [blue area]
Now do you see where this is going? The yellow and blue parallelograms
can be mapped to rectangles without changing their areas. Take the
difference of their areas, and we are left with the area of rectangle PQRS.
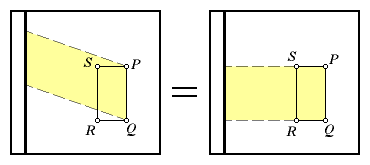
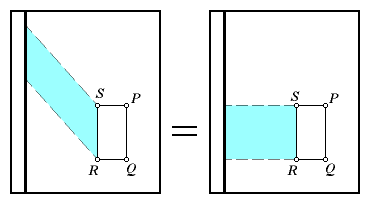
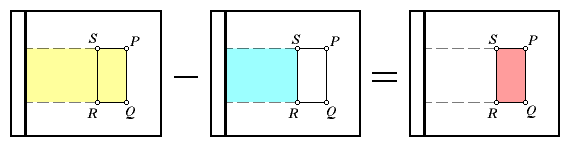
What was proved here?
I know, I know. It looks like a lot of hand waving so far. The planimeter
in this model does not even have the same construction as the one in the
picture. I said that I would get back to that, and I will, but not right
now. Also, I said that this instrument would measure the area of irregularly
shaped regions, but I only proved that my modified instrument (which is called a linear planimeter) would work
for a rectangle that is oriented square with the runner. What about that
irregular region?
Refer to the region below, with the sinuous boundary. A nice thing about
rectangles is that they can be stacked together in such as way that they
will tile a plane, leaving no gaps between the rectangles. There are gaps
between the rectangles and the blue boundary, but by constructing smaller
and smaller rectangles, those gaps become as small as we wish.
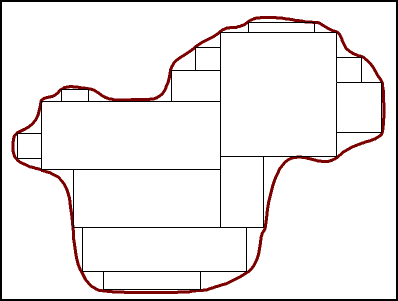
Now, using the linear planimeter, trace one rectangle. Lift the planimeter
so that the wheel does not move. Place it down on a second rectangle, and
trace it. Continue doing this until all of the rectangles have been traced.
The scale will show an accurate area for the region.
This process will work, but it is not at all practical. There is too
much lifting and moving. Fortunately, there is a way to simplify the routine.
Notice that each of the interior line segments was traced exactly twice. In fact, they were traced in opposite directions, effectively canceling
any change in the instrument's scale. That means that we could just as
well skip all of the interior courses.
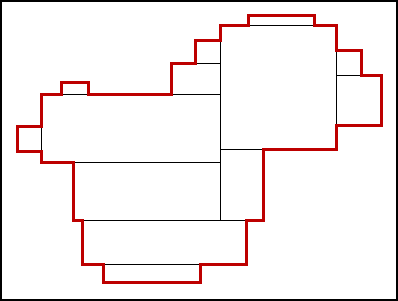
What we need to be tracing is the perimeter courses, highlighted in
red here. Of course, it would be more accurate if we fill in those gaps
with smaller rectangles. As we fill more and more of the gaps, this red
boundary takes the shape of the original boundary. In other words,
we could save a lot of work by forgetting all of the rectangles and simply
tracing the boundary. That is exactly how a planimeter is used.
But what about a polar planimeter?
This part is being saved for last because it requires calculus. If you are willing to accept my word that the length of the blue anchor arm does not matter, then the explanation above may give you a conceptual understanding of the planimeter.
In this sketch we have a planimeter tracing a boundary. Notice that the path of point B is restricted to a circle. For now, forget about the area of the region. Concentrate on the area that is covered by the green arm. Take the arbitrarily small subregion covered as the planimeter goes from C to C'. Call its area dw.
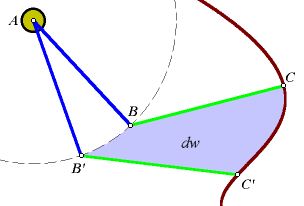
We know how to compute the area when the green arm is sliding, but in this case, it is sliding and turning at the same time. It will help to separate the components of this motion. First let the arm pivot, so that it is parallel to B'C'. Construct point E to show this first step. Now let the arm slide the rest of the way to B'C'. The subregion is now shown as a pentagon, BCEC'B'.
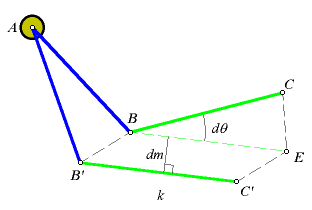
Let dθ be the rotation of the arm as it goes from C to E. Let dm be the change in the scale reading only while the arm is sliding. The scale also moves when the arm rotates, but that will be addressed later. As before, k is the length of the green arm. The area of the subregion can now be expressed algebraically. Some of these area formulas may appear to be approximations, but remember, both dθ and dm are arbitrarily small.
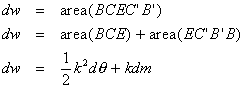
By integrating as the planimeter traces the entire region, we can get a formula for W, the area of the region crossed by the green arm when the planimeter makes one complete circuit around the region.
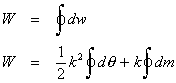
The first term in this formula integrates the angle change as the pointer traces the entire region. Since the planimeter begins and ends in the same position, the net change in the angle is zero. Therefore, the changes in the scale reading caused by rotation have no influence on the final reading.
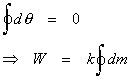
Remember that dm was defined as the movement of the scale due to the sliding of the arm. This is the only thing reflected in the area equation. The integration of dm over the entire circuit is simply the net change in the scale, in other words, the final scale reading. Let M be the final scale reading.
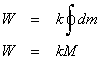
Of course, what we computed was the area crossed by the green arm, not the area of the region that was traced. Think again. When the arm is sliding backwards, the scale is moving backwards. In that case, the area it is covering is subtracted from the total. When the planimeter traces a region, the arm makes a broad sweep, then backs over the part that is outside of the region.
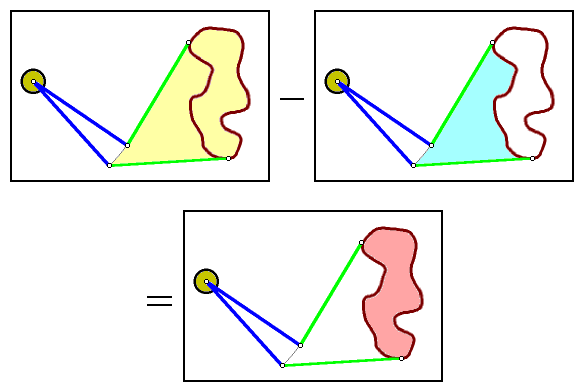
In fact, some of the parts may be covered more than twice. Work it out. The exterior region will be covered an even number of times, alternating signs each time. The interior is covered an odd number of times, with a net equivalent of being crossed once in the positive direction.
There is still one more loose end. As I said earlier, the length of the blue arm is immaterial, and I proved it mathematically and experimentally. For the experimental part, I simply taped an extension onto the arm and compared the results. How was it proved mathematically? Go back through the calculations. At no time did we need to specify the length of the blue arm. If we can compute the area without knowing the arm length, then it does not matter what that length is. However, the length must be constant (Why?), and of course, the pointer must be able to reach all points on the boundary.
Will the planimeter work if the anchor point is within the region being measured?
Why or why not?
German Adaptation
Content from this page has been adapted and merged into a German language article by Wolf-G. Blümich. It can be accessed at the link below.
Das Planimeter
Back to Whistler Alley Mathematics
Last update: January 8, 2012 ... Paul Kunkel whistling@whistleralley.com
For email to reach me, the word geometry must appear in the body of the message.