A few of these lessons have employed inversion geometry, so it seemed to make sense to write something on the subject. This is not a thorough treatment of the subject, but it might do for an introduction or a brush-up. First, a definition of inversion:
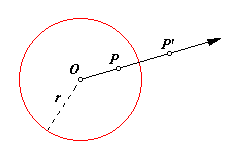
Consider a circle with center O and radius r. If point P is not O, the inverse of P with respect to the circle is the point P′ lying on ray OP such that (OP)(OP′) = r2. The circle is called the circle of inversion, and point O is the center of inversion.
Look at the equation again and see how many simple conclusions may be drawn from it:
(OP)(OP′) = r2
|
If (OP)(OP′) = r2, then (OP′)(OP) = r2. |
If point P′ is the inverse of P, then P is the inverse of P′. |
|
If OP < r, then OP′ > r |
If a point is on the interior of the circle of inversion, then its inverse is on the exterior. |
|
If OP > r, then OP′ < r |
If a point is on the exterior of the circle of inversion, then its inverse is on the interior. |
|
If OP = r, then OP′ = r |
If a point is on the circle of inversion, then so is its inverse. This is an invariant point. The point is its own inverse. |
An inversion effectively turns the circle inside out. Every point on the inside goes outside, every point on the outside goes inside, and all of the points on the circle itself stay put. The only thing unaccounted for is the center of the circle. Let us say that it goes to a point at infinity.
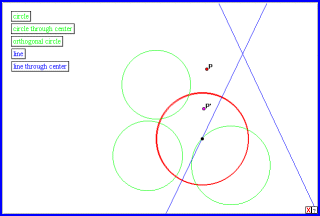
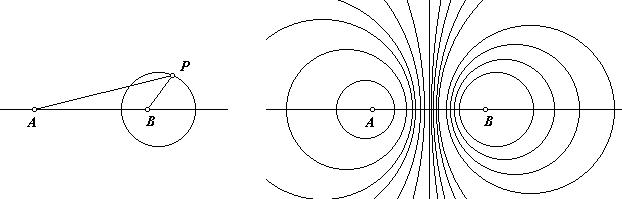
Click on the image below to activate an interactive Java sketch. Point P may be moved freely. Its inverse, P′, is traced. Watch the path of the inverse as point P traces several paths.
Notice that when point P traces a line in the animated sketch, the trace of its inverse is discontinuous. This is because P cannot be made to trace the entire line, which is, of course, limitless.
Here are six propositions. The first five may be inferred from observing that animated sketch.
Now the proofs:
The inverse of a circle (not through the center of inversion) is a circle.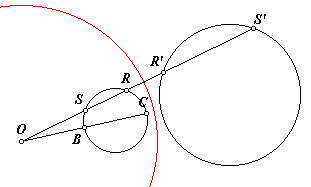
In this sketch, the circle on the left is being inverted with respect to the red circle, with center O and radius r. The line segment OC includes BC, a diameter of a circle. As point R traces the circle, ray OR intercepts the circle at points R and S. Points R′ and S′ are their respective images.
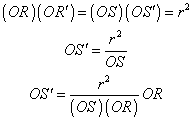
At this point, we can use the substitution (OS)( OR) = (OB)( OC). Do you see why this is true?
![]()
This shows that point R′ is the dilation of R with point O the center of dilation and r2/[(OB)( OC)] the dilation ratio. The line segments OB and OC will have constant measures, no matter where point R is. This makes the dilation ratio constant, so the locus of point S′ is a dilation of the circular path traced by R, meaning that S′ too must trace a circle. But point S′ also is the inverse of point S, which traces the same circle. Therefore, the inverse of the circle is another circle.
The inverse of a circle through the center of inversion is a line.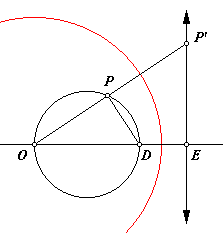
Again, point O is the center of inversion and r is the radius. Point P traces a circle through O, and P′ is its inversion. Let OD be a diameter of the circle. There must be some point E on ray OD such that (OD)(OE) = r2. It will be shown that the triangles POD and EOP′ are similar.
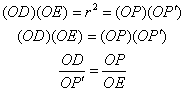
This shows that two pairs of corresponding sides of the triangles are proportional. The triangles share the same included angle, ∠POD. By side-angle-side, the triangles are similar. Since ∠OPD is inscribed in a semicircle, it is a right angle, and so is its corresponding angle, ∠OEP′. This means that point P′ must be on the line through point E and perpendicular to the line OE. There is only one such line, so it is traced by point P′.
What happens when point P reaches point O, the center of inversion? The inversion of point O has been defined as a point at infinity. This gives us some consistency because as P approaches O from one side or the other, P′ approaches the limit of the line, that limit also being a point at infinity.
The inverse of a line (not through the center of inversion) is a circle through the center of inversion.
This will be left as an exercise. Try taking the previous proof and working backwards.
A circle orthogonal to the circle of inversion is its own inverse.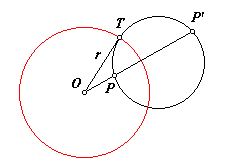
This is a quick one if you look at it in the right way. In the image at right, O(r) is the circle of inversion. The other circle is orthogonal to it. Point T is one of the intersection points of the two circles. Since the circles are orthogonal, radius OT must be tangent to the second circle. From point O construct a secant intersecting the other circle at points P and P′. The product of the two secant distances is equal to the square of the tangent distance.
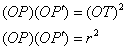
Therefore, points P and P′ are inverses of each other. The points where the circles intersect are both on the circle of inversion and are therefore their own inverses.
This shows that a circle orthogonal to the circle of inversion is invariant. Actually, the intersections are the only two invariant points, but the image of the circle is in fact the same circle.
A line through the center of inversion is its own inverse.
This makes a line through the center of inversion invariant. The proof of this proposition is left to the reader. One intuitive way of looking at it is to consider a line through the center a limiting case of an orthogonal circle.
Angles are preserved in inversion.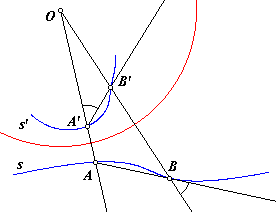
The angle of intersection between two curves is the angle of intersection of their respective tangents at the point of intersection (if in fact they have tangents at that point). This applies to lines, circles, or any other curves. Let us first show that the angle of intersection between a curve and a radial from the center of intersection is preserved.
In the image at right, s is a curve, points A and B are on s, and s′, A′, and B′ are their respective inversions. First, show that triangle AOB is similar to triangle B′OA′. Then, it can be shown that the two marked angles must be congruent.
Now, suppose that point B is a sliding point attached to s. What happens as B approaches A? Lines AB and A′B′ approach tangency to their respective curves. One of those marked angles approaches the angle of intersection between s and radial OA while the other approaches its inverse.
But what about the angle of intersection between two curves? Introduce another curve intersecting s at point A and go from there.
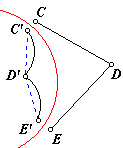
Here is a word of caution. Points C, D, and E are inverted to C′, D′, and E′. Does this mean that ∠CDE is congruent to ∠C′D′E′? Certainly not. This counterexample should make it clear. It appears that ∠CDE is acute, but ∠C′D′E′ is nearly 180 degrees. Line segments DC and DE are inverted into arcs. The inverse of the angle is the angle at which the arcs intersect, not the angle of intersection of the chords.
Apollonian circle - Consider points A and B, and some constant k. Find point P such that (AP) = k(BP). The locus of points satisfying this condition is an Apollonian circle. For any two points, there are infinitely many Apollonian circles, one for each distinct value of k. When k = 1, The circle becomes a line, the perpendicular bisector of segment AB. Each of the circles divides AB harmonically.
harmonic division - Points C and D divide line segment AB harmonically if points C and D are on line AB and the following proportion is satisfied:
![]()
![]()
If points C and D divide segment AB harmonically, it follows that points A and B divide segment CD harmonically.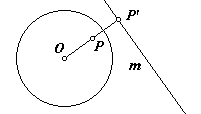
polar/pole - Consider a circle of inversion with center point O. Points P and P′ are inverses of each other. Line m contains point P′ and is perpendicular to line OP′. Line m is the polar of point P, and point P is the pole of line m. The polar of point O is a line at infinity, and the pole of a line containing O is a point at infinity. In this way, every line in the extended plane is mapped to a point and every point is mapped to a line.
mid-circle - Given two circles, a mid-circle is a circle of inversion such that the circles are inverses of each other. Non-congruent circles that intersect have two mid-circles. There is a limiting case of two congruent circles whose mid-circle becomes a line, the perpendicular bisector of the segment joining the two center points. In this case, inversion becomes reflection on the line.

radical axis - The radical axis of two circles is the line that contains the center points for all circles that are orthogonal to both of the given circles. If the given circles do not intersect, then all of the orthogonal circles that are centered on the radical axis intersect each other at the same two points. The radical axis of intersecting circles is their common secant, and the orthogonal circles do not intersect each other.
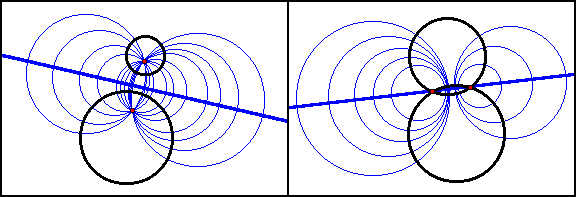
On the left, the common chord of the family of orthogonal circles is divided harmonically by each of the two given black circles, which are circles of Apollonius for the two red points. On the right, the common chord of the given circles is divided harmonically by each of the orthogonal blue circles, and it is the blue circles that are circles of Apollonius.
radical center - The radical center of three circles is the center of the circle that is orthogonal to all three of them. It is the intersection of the three radical axes formed when the circles are taken in pairs.
Those of you who are using the Geometer’s Sketchpad may have some use for the tool file below. It includes tools for constructing most of the objects that were presented on this page.
Back to Whistler Alley Mathematics