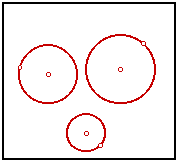
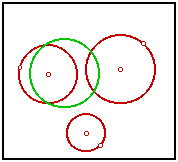
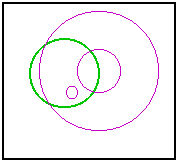
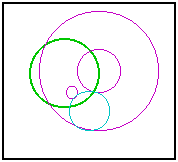
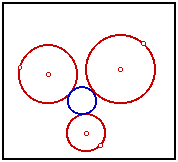
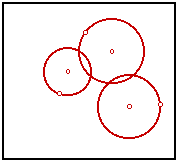
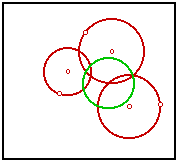
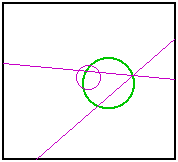
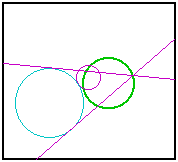
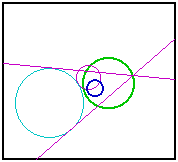
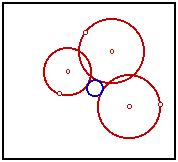
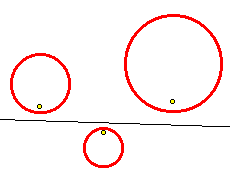
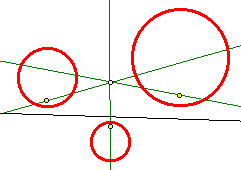
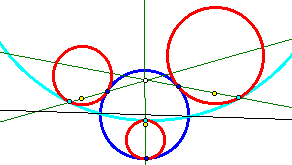
Tangent Circles

In an earlier sketch, I tackled a classic problem of Apollonius: Construct a circle tangent to three arbitrary circles. I was later advised by an acquaintance, John Del Grande, that my solution was incomplete. A circle may be seen as a point or a line, these being the limiting cases as the radius approaches zero or infinity. Rather than use three circles, we should be using any combination of three from points, lines, and circles.

Dr. Del Grande listed all of the ten combinations in a textbook, Mathematics 12, by J. J. Del Grande, G. F. D. Duff, and J. C. Egsgard (1965 W. J. Gage Limited).

The developers of The Geometer’s Sketchpad have been working to make Sketchpad documents that can be viewed on a web browser. Thanks to their efforts, the ten images immediately below are dynamic geometry images. The independent objects are red. The constructed circles are blue. If an independent object is a circle, then it may be manipulated by moving its center, or by moving a point on the circle, which controls the radius. If the independent object is a line, then it is controlled by two points on the line. Independent points may be moved freely.

Copyright © 2015 KCP Technologies, a McGraw-Hill Education Company. All rights reserved.
Release: 2015Q2-1, Semantic Version: 4.2.1, Build Number: 911.7-r, Build Stamp: dn.kcptech.com/20150724142440

Three Circles

At most, eight solutions.
 

Two Circles, One Line

At most, eight solutions.
 

Two Circles, One Point

At most, four solutions.
 

One Circle, Two Lines

At most, eight solutions.
 

One Circle, One Line, One Point

At most, four solutions.
 

One Circle, Two Points

At most, two solutions.
 

Three Lines

At most, four solutions.
 

Two Lines, One Point

At most, two solutions.
 

One Line, Two Points

At most, two solutions.
 

Three Points

At most, one solution.
 

Construction Notes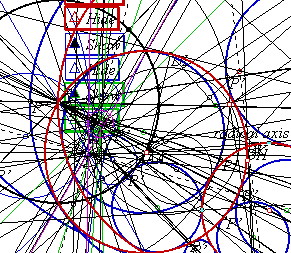

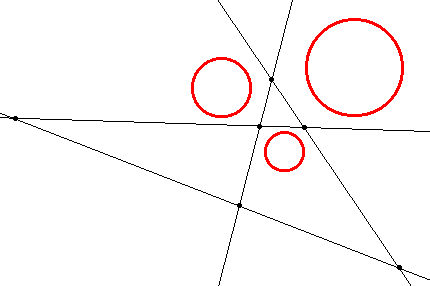
That last construction is simply a circle through three points. It is covered in most elementary geometry courses. Some of the other constructions are extremely complicated. If you doubt that, then open the Sketchpad version of the Three Circles drawing and execute the Show All Hidden command. You will see something similar to the picture at right. This is one case in which it is difficult to dispute the value of dynamic geometry software. With so many interdependent objects, I would never be able to complete this drawing using straightedge and compass. It would be too difficult to distinguish between the different objects, the precision would be compromised with each step, and so many construction marks could not be cleanly erased.

Inversion geometry is used in the more difficult constructions. If you have never studied it, or if you need a refresher on the terminology, this link may be helpful: Inversion Geometry

This begins with my own construction. I later learned of several others, at least one of which is much more elegant. This one comes first, however, because it is my own.

It would seem difficult to find a circle that is tangent to three given circles, but if two of those circles were concentric, then it would not be so difficult at all. Given any two non-intersecting circles, it is possible to define an inversion such that the circles’ images are concentric. Invert all three circles, construct tangent circles, and run the solutions through the same transformation. Their images will be tangent to the original circles.

Begin with three circles.

Define the inversion.

Invert the circles.

Construct a solution.

Invert the solution.

Take a bow.

What if the original circles intersect? That makes it even easier. Two intersecting circles can be inverted so that their images are intersecting lines. That would simplify the three-circle problem into a problem of two lines and one circle. Below is the same sequence of steps, beginning with intersecting circles.

The Gergonne Solution

Notice that the construction above is actually two constructions. The one to use depends on whether any of the given circles intersect. That would not have been such an issue in the third century BC, but we now live with dynamic geometry software, and the given conditions can change even after the construction is complete. It would be better to have one solution that fits all cases.

The construction below was published by Joseph-Diaz Gergonne in 1816. It too makes use of inversion geometry. One great advantage is that the same construction works for all but a few special configurations of the given circles. For three given circles, the Gergonne construction will render all solutions and will not result in any rogue circles, which are not solutions. This makes it work especially well with dynamic geometry. Do the construction once, and it will hold together while the arrangement of the given circles is changed.

Proof of the Gergonne solution can be found in the paper below. It is a journal article discussing solutions by François Viète, Isaac Newton, and Gergonne.

'The tangency problem of Apollonius: three looks',
BSHM Bulletin: Journal of the British Society for the History of Mathematics, 22:1, 34 - 46

The Gergonne construction: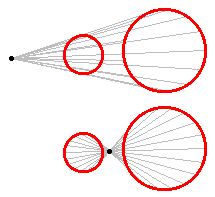

The dilation point or center of homothety of two circles is the point from which one of the circles may be dilated onto the other. For two circles, there are generally two dilation points.

From a set of three circles, three different pairs can be taken. For each pair, construct the two dilation points. That results in six points. Through these six points, it is possible to draw four lines, each containing three of the dilation points. Three of the lines separate one circle center from the other two centers. The fourth line has all three center points on the same side.


Each of these lines leads to as many as two solutions. For clarity, only one of the lines and two of the solutions will be presented here. Construct the poles of the line with respect to each of the three circles.

Construct the radical center of the three circles, and from that point, draw a line to each of the three poles. In this case, each line intersects its respective circle at two points.

The six intersection points are points of tangency for two solution circles, with three tangent points on each solution. The solutions can be constructed from these points of tangency.

Correctly separating them into groups of three may by a bit tricky. Here is one tip. If the line of similitude separates the center of one given circle from the centers of the other two, then the solution circle will do likewise. In this sketch, the center of the lower red circle is separated from the others by the line of similitude. Therefore, one solution circle is internally tangent to this odd circle and externally tangent to the others. The second solution, vice verse.

Geometer’s Sketchpad File

Below is a Geometer's Sketchpad document with constructed solutions for each of the ten cases. Most of the constructions are based on Gergonnes's solution.

Apollonius10.gsp

Back to Whistler Alley Mathematics

Last update: September 25, 2015 ... Paul Kunkel whistling@whistleralley.com
For email to reach me, the word geometry must appear in the body of the message.