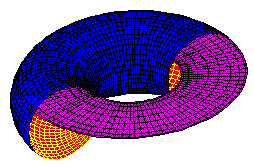
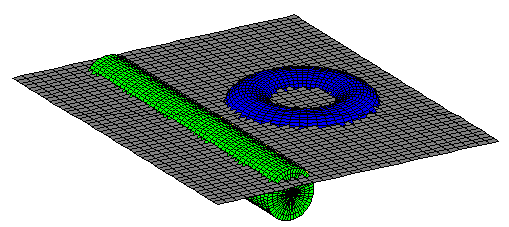
Volume of a Torus

I once received an email message from someone who wanted to know the volume of a torus. An interesting question, thought I. Actually, I had already been told the answer, but I had never bothered to investigate it and prove it. If I were to do this again, the easiest way probably would be to use Pappus’ Theorem for the volume of a solid of revolution. If you have not heard of it, look it up in a calculus text. It is not terribly complex, but it requires a good understanding of integral calculus.

As it happened, I did not use Pappus’ Theorem. Instead, I started by using a much less efficient method. In doing so, I stumbled onto a gem of an explanation. It is similar to a technique used by Archimedes (287-212 B.C.). He would often deduce geometric properties of a figure by comparing it with a simpler, better known figure. He would refer to planar regions, and ever line segments, as thought they had mass and weight. Archimedes deduced the volume of a sphere by comparing it with a cylinder and a cone. For an explanation of this, see the article “The Method of Archimedes” by John Del Grande, Mathematics Teacher 86(3), March 1993.

A torus is a solid of revolution. It is formed by rotating a circle about a line that is in the plane of the circle, but not intersecting the circle. A torus has the shape of a doughnut. Let r be the radius of the circle being rotated, and let R be the distance from the center of the circle to the axis of rotation.

Orient the torus so that its widest cross-section is aligned with the x-y plane. Now intersect the torus with a plane parallel with the x-y plane. What is the region of intersection?

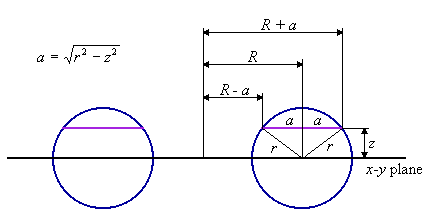
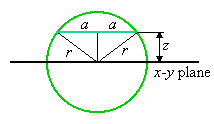
The intersection is a washer-shaped region called an annulus. It is the region between two concentric circles, so its area is the difference between the circle areas. Given the z-coordinate of the intersecting plane, we should be able to compute the area of the annulus. If we look at a cross-sectional view, we can see a simple relationship.

The radius of the interior circle is R-a, and the radius of the exterior circle is R+a, where .

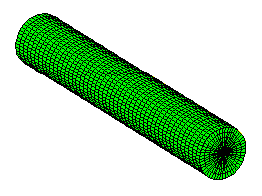
Now comes the comparison part. Here is a cylinder with radius r, and length 2pR. The cylinder’s axis lies in the x-y plane. See what happens when it is cut by the same plane that intersected the torus.

The plane’s intersection with the cylinder is a rectangle. Its length is 2pR, the same as the length of the cylinder. Notice that a cross-section of the cylinder is the same as a cross-section of the torus, because they have the same radius, r. So the width of the rectangle is 2a.

This is the same as the area of the annulus. For any z, a horizontal plane through z intersects equal areas with the torus and the cylinder, although their shapes are not at all similar. It can be imagined that arbitrarily thin slices are being shaved off of the torus and the cylinder, which are made of the same material. Each time the cutting plane passes through the solids, it cuts slices which are equal in area and thickness. If we pile the slices on oposite sides of balance scales, they must remain balanced. The objects have the same weight, hence the same volume. We already have a simple formula for the volume of a cylinder.

This is hardly a rigorous proof, but I am hoping that it conveys a qualitative understanding. The notion of cutting objects into thin, measurable slices is essentially what integral calculus does. Archimedes was practicing this method about 1900 years before the era of Leibnitz and Newton.

Back to Whistler Alley Mathematics