On The Square
The challenge: Given four arbitrary, unique points, A, B, C, and D, construct one line through each point such that the four lines form a square.
Take a minute and be sure that you understand the problem before you continue. If you have done this correctly, then each line includes at least one of the points and each point lies on at least one of the lines. The first time I heard it was at teachers’ conference. The conference speaker did not actually ask us to construct a solution; he asked us whether a solution was always possible. But the phrasing of the problem was more ambiguous. We quickly went to work in different directions, none of us quite understanding the rules. I produced a trivial example of a case in which it was not possible, but I did not understand that the sides of the
square were to be lines, not line segments. Then I showed a very simple construction, but I did not understand that each point had to be paired with a different line.
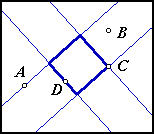
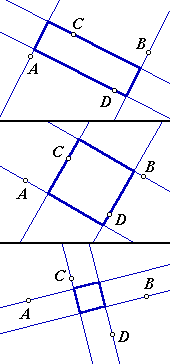
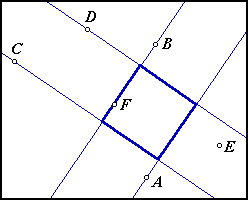
Here are three acceptable solutions:
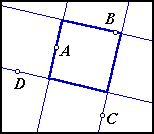 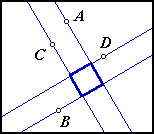 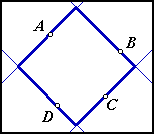
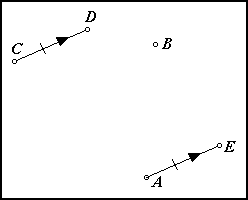
These two images do not show solutions:
 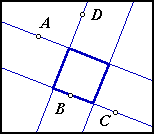
In the first image each of the sides includes one of the four points, but point B does not lie on a side. In the second image each point lies on a side, but there is one side that does not include any of the
four given points.
One of the lines must include point A, so imagine or draw some arbitrary line through A and call the line a. We can worry about its direction later. One of the lines must be parallel to a and must include one of the other points. So construct a parallel line through point B and call it b. The other two lines must be perpendicular to these lines and must include points C and D.
Construct these lines and call them c and d respectively. Did you end up with a square? As one of my instructors used to say, it is possible, with a probability of zero. Unless two of the lines are coincident, you should have a rectangle, and it is highly unlikely that the rectangle is a square.
 This whole construction was based on the four arbitrary points and line a. To change the position of any of the points would be cheating, but we can
change the direction of line a. As we do so, the dimensions of the rectangle change. This whole construction was based on the four arbitrary points and line a. To change the position of any of the points would be cheating, but we can
change the direction of line a. As we do so, the dimensions of the rectangle change.
On the animated image below dragging the point labeled drag will change the direction of line a. Lines b, c, and d will also change, since they are dependent on line a. The shape of the rectangle will cycle, repeating two times each time the controlling point goes through the circle. In each cycle, there are two positions in which a square is formed. Is this always true?
One dimension of the rectangle is the distance between lines a and b. That distance varies between zero and AB. Likewise, the other dimension of the rectangle varies between zero and CD.
If both of the dimensions are the same, then we have a square.
Try dragging the free points, A, B, C, and D. Is it possible to arrange them into positions such that there is never a square?
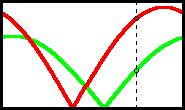 Now click on the button to show the graph. The red graph represents the distance between lines a and b. The green graph shows the distance between lines c and d. Only one cycle is shown, and both graphs have the same period. Both graphs touch the axis one time in each cycle, so clearly they must intersect. Generally, they will intersect two times in each cycle. Their intersections represent the positions at which the dimensions of the rectangle are equal. So, there are always two squares, right? Right? We’ll come back to that question later. Now click on the button to show the graph. The red graph represents the distance between lines a and b. The green graph shows the distance between lines c and d. Only one cycle is shown, and both graphs have the same period. Both graphs touch the axis one time in each cycle, so clearly they must intersect. Generally, they will intersect two times in each cycle. Their intersections represent the positions at which the dimensions of the rectangle are equal. So, there are always two squares, right? Right? We’ll come back to that question later.
There may be more than those two solutions. Remember how the rectangle was constructed. We started with line a through point A, and constructed a parallel line, b, through point B. So start
a different way. Construct parallel lines a and c and construct lines b and d perpendicular to them. That should result in two more solution squares. Now start again, this time with parallel lines a and d. That makes three pairs of squares, a total of six solutions.
Below is an outline of the construction for a typical solution:
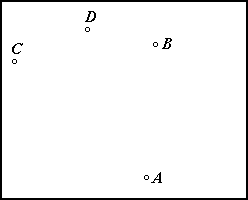
1) Begin with the four arbitrary points A, B, C, and D. |
2) Construct point E by translating point A by vector CD. |
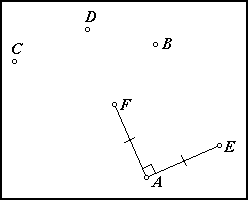
3) Rotate point E 90° about A. Let its image be point F. |
4) Construct line BF, and construct a parallel line through A. Through points C and D, construct lines perpendicular to line BF. |
The construction above delivers one of the solutions for which lines a and b are parallel. To get the other, change the angle of rotation to 270° in step 3. To get one of the other pairs, switch point B with either C or D.
Below is another animate image. This one shows all six solutions. The three pairs can be distinguished by color. By dragging the free points it can be seen that, under certain conditions, a pair of squares will diminish down to nothing. Why do they always vanish in pairs? What conditions cause them to vanish? Is it possible to make four squares vanish? All six squares?
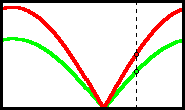 This situation was hinted at above. Go back to this previous animation, the one with the graph. It was suggested that with lines a and b parallel, there would always be two solutions because the graphs intersect twice in each cycle. That was not
entirely true. What if the graphs intersect where they both have a height of zero? If that is the case, the graphs actually meet only once per cycle, and the parallel lines are coincident. There is no such thing as a zero
by zero square, so this intersection does not represent a solution. This situation was hinted at above. Go back to this previous animation, the one with the graph. It was suggested that with lines a and b parallel, there would always be two solutions because the graphs intersect twice in each cycle. That was not
entirely true. What if the graphs intersect where they both have a height of zero? If that is the case, the graphs actually meet only once per cycle, and the parallel lines are coincident. There is no such thing as a zero
by zero square, so this intersection does not represent a solution.
What condition causes this? A little experimentation (or better yet, reasoning) will show that this happens when lines AB and CD are perpendicular. Move the points into such a position and drag the point
that controls the directions of the lines. You will see some interesting behavior in the rectangle formed by the line intersections. It changes size, but the length/width ratio remains constant. This prevents it from becoming a square.
There may still be solutions even if lines AB and CD are perpendicular. Instead of having line a parallel with line b, make lines a and c parallel. This will produce a pair of
solutions, unless it is also true that lines AC and BD are perpendicular. What if they are perpendicular? Can we still solve the problem by pairing points A and D and making line a parallel with line d? No, we cannot. If 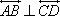 and and 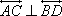 , then points A, B, C, and D form an orthocentric system, and it follows that , then points A, B, C, and D form an orthocentric system, and it follows that 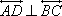 . This is why on the six-square sketch it is possible to make two solutions or all six solutions vanish, but it is not possible to make exactly four solutions vanish. See my Orthocenter page
for more information on orthocentric systems. . This is why on the six-square sketch it is possible to make two solutions or all six solutions vanish, but it is not possible to make exactly four solutions vanish. See my Orthocenter page
for more information on orthocentric systems.
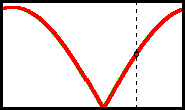 So, it appears that there are always solutions unless the four points form an orthocentric system. There is still hope though. Go back again to the
sketch with the graph. Arrange the points so that So, it appears that there are always solutions unless the four points form an orthocentric system. There is still hope though. Go back again to the
sketch with the graph. Arrange the points so that 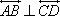 . The two
graphs have the same period and zero phase shift, which makes them intersect when both have a height of zero. But what if they also have the same amplitude? In that case, the graphs are coincident. The length and width of the rectangle are equal no matter what direction is chosen for the lines. There are infinitely many solutions. To create this arrangement, lines AB and CD must be perpendicular and AB must equal CD. . The two
graphs have the same period and zero phase shift, which makes them intersect when both have a height of zero. But what if they also have the same amplitude? In that case, the graphs are coincident. The length and width of the rectangle are equal no matter what direction is chosen for the lines. There are infinitely many solutions. To create this arrangement, lines AB and CD must be perpendicular and AB must equal CD.
Can this be done with an orthocentric system? Below is yet another animated sketch. This one forces an orthocentric system. Points A, B, and C are free. Point D is the orthocenter of ΔABC. The three colors represent attempts with line a paired with b (blue), c
(red), or d (green). Notice that when the line directions are changed, the rectangles change in size, but their length/width ratios do not change. Clicking one of the Square buttons will move point C to a position that causes one of the rectangles to become a square.
To begin with, stay away from the black Show loci button. Here is the challenge: If we move only point C, point D will automatically be moved to preserve the orthocentric relationship. Where can point C go to allow a solution? Is it possible for two of the colors to have solutions at the same time? All three?
Clicking Show loci will show the locus of points that C can occupy to create a solution. Why does this work? Are there any other possibilities?
Conclusions
The four-point square construction is always possible if the four points do not form an orthocentric system. Generally there are six solutions. If two disjoint pairs of points define perpendicular lines, there generally
are four solutions. However, if the same two pairs are equidistant, then there are infinitely many solutions.
The construction is impossible only if the four points form an orthocentric system. In such cases there generally is no solution, but if two disjoint pairs of points are equidistant, then there are infinitely many solutions.
Interestingly, the construction method described above fails only if there are no solutions or infinitely many solutions.
Web Sketchpad Files
The animated sketches on this page were created with Web Sketchpad, a developmental version of The Geometer’s Sketchpad.
|