Rungs and Vineyards

The Rungs

The image at the top of this page is an animated GIF. It simulates an interesting visual phenomenon, one which you may have observed yourself. I used to always notice it when I lived in Anacortes, Washington, which is on Fidalgo Island, on Rosario Strait. The island is separated from the mainland by a narrow channel, and Route 20 has a bridge crossing the channel. On the north side of that bridge is a pedestrian path with guardrails on both sides. The rails have uniformly spaced, vertical rungs.

If you live near that bridge, go watch what happens when you drive across it at 55 miles per hour (advisable, since it is a speed trap). You are looking through both guardrails at the same time. At that speed, it is difficult to see any individual rungs. They become blurred. There is the illusion of much larger rungs, widely spaced. You can see between them, but you cannot see through them. What’s more, these phantom rungs appear to be moving with the car. What causes that?

The animated GIF shows a perspective sketch of two rows of rungs moving left to right. It may help to stand back a few feet from the screen. You should see the illusion of several stationary objects, although all of the objects are in motion. Open the Java applet rungsani.htm. It allows you to change the perspective of the observer, and the size and spacing of the rungs.

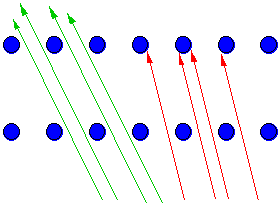
Let us consider what it is that prevents us from seeing through both rows. In this illustration, we see an overhead view of the two rows of rungs. The pedestrian path is between them. Of course it is possible to see through a single row. Simply look between the rungs. The green arrows represent parallel sight lines. They are oriented in a direction such that each rung on the north row is directly behind a rung on the south row. Looking in this direction, the north row cannot even be seen, so it is easy to find an unobstructed view.

Now look at the red arrows. They too are parallel sight lines, but with a different orientation. This time the rungs of the north row line up with the spaces of the south row. Even if you look between the south rungs, your line of sight will probably be obstructed by one of the north rungs.

It appears the sight lines will be the clearest when we look in a direction such that the rungs of one row line up with the rungs of the other row. The direction of sight is what matters, not our position on the bridge. That is why the phantom obstructions appear to be moving with the car.

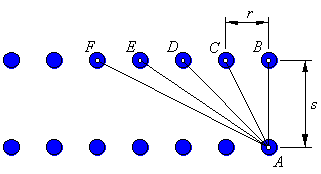
Can we compute a formula for the directions of the sight windows? Clearly, if we look directly north, perpendicular to the guardrails, the rungs will line up. That would be the direction from A to B in the sketch above. Now turn to the left. The rungs will not line up again until we look in a direction parallel to AC. The angle we turned is ∠BAC. What is the measure of that angle (the northwest bearing)? Let r be the space between the rungs, and let s be the distance between the guardrails.

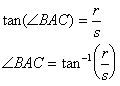
There are other sight windows. We could look in a direction parallel to AD, or AE, or AF. To find those bearings, compute the measures of ∠BAD, ∠BAE, and ∠BAF. Those angles are tan^-1(2r/s), tan^-1(3r/s), and tan^-1(4r/s). In fact, there will be a sight window at angle tan^-1(nr/s), for any integer n. The angles between these windows will not be equal, but, from our perspective, they appear to be evenly spaced along the bridge.

What happens to the visual effect if we get further away from the guardrails?

What would happen if the rung spacing on one guardrail were slightly different than the spacing on the other?

The illusion created by this situation is called a moiré effect. In this case, its occurrence was incidental. Research moiré effect to find how similar illusions can be created purposely.

Extension:

This is something I noticed a few weeks after I wrote the explanation above. Look at this photograph. It is the belfry of Gerberding Hall, on the University of Washington campus. The openings are covered with steel webbing in order to keep out the pigeons and bats. Look closely through the opening. You are looking through two layers of the webbing. One is closer than the other. The pattern of the webbing is much too small to see at this distance, but the two layers create an interference pattern, which is very noticable.

The image at right is an approximation of the pattern of the webbing. If you have the Geometer’s Sketchpad, or some other appropriate software, try duplicating the pattern. Then dilate it by a factor of, say, 1.2. When the two patterns are overlaid, it should create an interference effect similar to the one in the belfry. Try the same thing with other patterns, such as a square grid, or a honeycomb.

The Vineyards

Here is a related topic. This one I noticed while driving through California on Highway 101. It’s remarkable that I have such a clean driving record when I pay so little attention to the road. So anyway, 101 goes through a lot of vineyards and orchards. They are always laid out in a square grid pattern. Maybe that is the most efficient use of space. Whatever the reason, it must be important to them, because the plants appear to have been staked very precisely.

When I drive by and look straight up to rows, they appear to open up. In that direction, I can follow a row, with my eyes, all the way to the end of the field. Try it yourself. If you keep looking in that direction, all of the rows will go past and open up right there. This is an effect I used to notice with the corn rows in my native Illinois. But in the vineyards, it gets even better. You can turn your eyes 45° and see a similar effect along the diagonals. Next try looking up one plant and over two. You will see rows of plants in that direction too. In fact, if you can line up any two plants, you will see a whole row of plants in that direction, but some are easier to see than others.

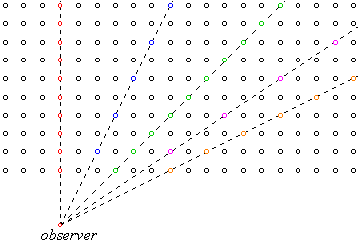
The first sketch below is an overhead view of the vineyard. Below it is a perspective drawing of the same vineyard, viewed from a point just above the tops of the plants. Same of the plants that line up are color coded, so that they can be seen in both sketches. When they line up, they appear as a single vertical line in the perspective drawing.

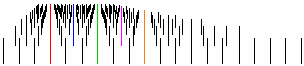
There is a Sketchpad file to go with this one too. Open vineyard.htm and experiment with it. Change the position of the observer, and change the heights of the eye level and the plants. When you move the observer across the screen, it should look similar to the vineyard viewed from a moving car. It is even possible to drive through the vineyard, but please do not attempt this in real life.

If you are looking for practical applications, you may be reading the wrong web page. I brought this up only because I find it interesting. Here are a few things to think about.

Assume a vineyard on a plane infinitely wide and deep. Is it possible to find a row of plants for any given direction?

How can these plant rows be used to model the set of rational numbers?

Perspective

Both of the Sketchpad files on this page have perspective drawings. The astute observer will have noticed that they are quite different. rungsani.htm was used for the animated drawing at the top of the page. See how the rungs grow in size as they get closer to the observer. But what about vineyard.htm? All of the plants in the front row have the same height, but if they lie on the same line, they cannot all be the same distance from the observer. Which is correct? Neither. Which is better? Take your pick.

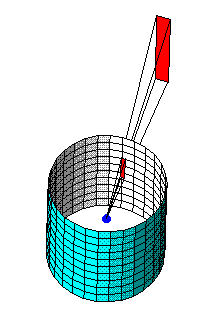
The sketch of the rungs approximated a cylindrical projection. Imagine the observer as a point on the axis of a vertical cylinder. Now consider a ray, originating at the observer and passing through a point on the object to be plotted. That point will be projected to the point where the ray intersects the cylinder. After all of the points of interest have been projected onto the cylinder, it is unrolled and laid flat.

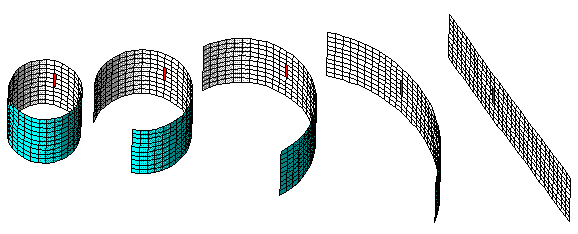
The vineyard was drawn using a planar projection. This concept is a bit simpler. Have the ray intersect a plane instead of a cylinder. The Sketchpad file creates the projection mathematically, but you can easily create one optically. With one eye open, look out a window. Hold your head perfectly still, and trace outside objects onto the glass. The drawing is a planar projection.

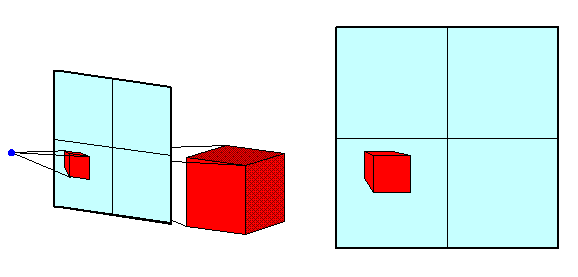
In the vineyard drawings, the images of all of the plants in the front row have the same height, even though some are further away than others. But the images of the plants in the back rows are smaller, just as we would expect. Why is that?

In the cylindrical projection, will all straight lines be projected as straight lines? Which lines will and which will not? What about the planar projection?

Could you create one of these projections from the other?

Consider the advantages of each of these projections. Cartographers use planar and cylindrical projections, and many others, to represent a curved surface (Earth and other planets) on a flat map. Many of their projections cannot be described with a simple geometric model.

Geometer’s Sketchpad Files

The Java applets presented here were created with the Geometer’s Sketchpad (version 3). The original Sketchpad files may be downloaded here:

rungs.gsp

vineyard.gsp

Back to Whistler Alley Mathematics