The Icosahedron

The icosahedron has 20 equilateral triangular faces, 12 vertices, and 30 edges. Five faces meet at each vertex.

For the calculations that follow, consider an icosahedron of side length s.

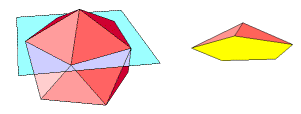
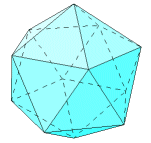
The dihedral angle formula being used in these pages applies only to cases in which exactly three faces meet at a vertex. In the case of the icosahedron, five faces meet at each vertex. Cut away the five faces that meet at a single vertex. This forms a pyramid with a regular pentagonal base. At a base vertex, three faces meet, two triangles and a pentagon. The dihedral angle between the two triangles is the same as that between the faces of the icosahedron. The formula can be applied with α = β = π/3 and γ = 3π/5. The pentagon is an interesting study in itself. Follow this link for an explanation of some useful properties of the regular pentagon: Pentagon Properties

Compute the apothem of a triangular face. Use it to find the inradius and circumradius of the icosahedron.

The surface area is 20 times the area of a single triangular face.

Apply the volume formula.

Other Properties

The icosahedron has 120 symmetries.

The icosahedron is the dual of the dodecahedron. Connect the centers of adjacent faces of the icosahedron, and the result is a dodecahedron. Connecting the centers of faces of a dodecahedron results in an icosahedron.

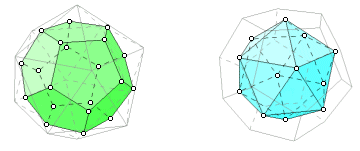
A tetrahedron or a cube can be formed by connecting centers of icosahedron faces. An octahedron can be formed by connecting midpoints of edges.

A cross-section of an icosahedron can be a regular pentagon or a regular decagon.

A planar projection of the icosahedron can be a regular hexagon or a regular decagon.

Back to the Platonic Solids