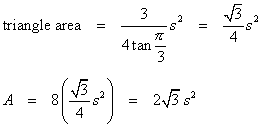
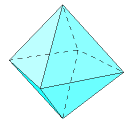
The octahedron has 8 equilateral triangular faces, 6 vertices, and 12 edges. Four faces meet at each vertex. The octahedron might also be classified as a square dipyramid or a triangular antiprism.
Consider an octahedron with side length s.
The faces are equilateral triangles. Find the area of one face. Multiply that by the number of faces for the total surface area.
|
|
There is a problem with the dihedral angle formula being use in these pages. It applies only to cases in which exactly three faces meet at a vertex. Here, we have four. Consider this. Four faces that meet at a common vertex are cut away from the rest of the solid. The result is a pyramid with a square base. At each of the base vertices there are three faces, including two triangles and a square. The dihedral angle between the two triangles is the dihedral angle of the octahedron. We can now apply the formula. Let
|
|
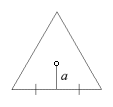
Next, find the apothem of an equilateral triangle, and use it to find the inradius and circumradius of the octahedron.
|
|
|
|
Another way with the volume is to dissect the octahedron into two pyramids. Each has a unit square for a base and a height equal to the circumradius.
The octahedron has 48 symmetries.
The octahedron is the dual of the cube. Connect the centers of adjacent faces, and the result is a cube. Do the same to a cube, and the result is an octahedron.
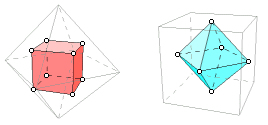
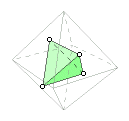
A tetrahedron can be formed by connecting centers of certain faces of the octahedron. This fact follows naturally from its dual relation with the cube.
A cross-section of the octahedron can be a square or a regular hexagon.
|
|
|
A planar projection also may be a square or a regular hexagon.
|
|
|
|
|
|
|
|
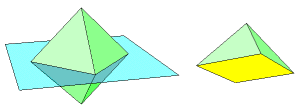
Here is an interesting property. Lay an octahedron on a horizontal surface. It is possible to lay a tetrahedron on the same surface and nestle it right underneath the octahedron. This follows from the fact that their dihedral angles are supplementary. |
Push them together. The common face goes away. Less obvious is the fact that three other pairs of faces are coplanar. Edges vanish, and it becomes a heptahedron, having three rhombic faces and four triangular faces. |
|
|
|
|
|
|
Start over again with a single octahedron. Attach a tetrahedron to each of its eight faces. |
The result is this stellated octahedron. It might also be visualized as two intersecting tetrahedra. |
|
|
|
|
|
|
Now fit twelve octahedra around this figure. They will fit perfectly. |
Here is the result of that last step. It is ready for another layer of tetrahedra. Together, the octahedron and tetrahedron pack space, but neither of them can do so alone. |