The Cube

The cube might also be called a regular hexahedron. It has 6 square faces, 8 vertices, and 12 edges. Three faces meet at each vertex.

Of the Platonic solids, the cube does not have the least number of faces or vertices, but it is surely the simplest by any other measure. For that reason, this page will not waste too much effort on tedious derivations of obvious measures. In the following, we consider a cube of edge length s.

 

area of each face  =  s2

Each face is a square of side length s.

 

A  =  6s2

because there are six faces

 

Each edge is perpendicular to the adjacent edges, so this follows from the definition of the diheral angle.

 

 

The distance between two opposite faces can be measured along an edge, so s is the diameter of the inscribed sphere. The inradius must be half of that.

 

 

V  =  s3

Other Properties

The cube has 48 symmetries.

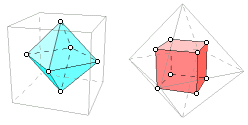
The cube is the dual of the octahedron. Connecting the centers of the adjacent faces of a cube results in an octahedron, and vice verse.

One other Platonic solid can be found inside the cube. Pick four of the vertices and fit a tetrahedron.

A cross-section of a cube can be an equilateral triangle, a square, or a regular hexagon.

A planar projection of a cube can be a square or a regular hexagon.

Here is an interesting physical property. Pick up a cubic playing die, and twirl it like a top. Although it does not have radial symmetry, it will seek a vertical axis through two opposite vertices.

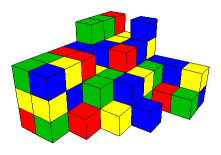Finally, here is a property that is important in design. The cube packs space. It is the only Platonic solid with this property. Buildings, books, appliances, and containers all tend to be in the shape of rectangular prisms (not necessarily cubes). This is not because designers lack imagination. Things just fit better that way. For efficient use of area and space it is hard to beat a right angle.

Watch this space for more on space filling solids.

Back to the Platonic Solids

Last update: June 3, 2026 ... Paul Kunkel whistling@whistleralley.com
For email to reach me, the word geometry must appear in the body of the message.