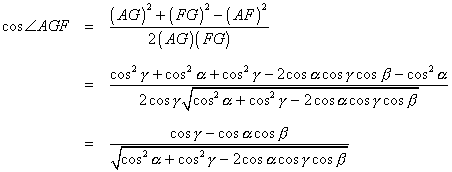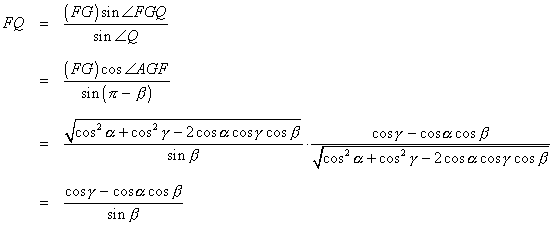Formula Derivations for Polyhedra

The Whistler Alley pages addressing Platonic solids make repeated use of several formulas. Those formulas and their derivations are explained more thoroughly below.

The Dihedral Angle

A dihedral angle is the angle of intersection of two planes. It is the measure of an angle having its vertex on the intersecting edge and one side in each of the planes. The sides of the angle are perpendicular to the intersecting edge.

In the context of polyhedra, a dihedral angle is the angle of intersection of two adjacent faces. For each of the Platonic solids, there is only one dihedral angle, because all pairs of adjacent faces intersect at the same angle.

A vertex of a polyhedron is at the intersection of three or more faces. In the case of three, there is a convenient formula for the dihedral angles. If the three faces fit together at all (they might not), there is only one way. Take this example. Three polygons share the common vertex A. The polygon angles at A are α, β, and γ, which are not necessarily equal. The polygons shown here are triangles, but they could have any number of sides. For this formula derivation let it be assumed that α, β, and γ are all acute angles. (See other cases below.)

Start with the faces laid out in a net in a horizontal plane. The net is hinged on sides AB and AC. Points D and E swing up and meet at point P. Point P is projected downward to point Q, on the horizontal plane (not necessarily on polygon ABC). In order for the points to meet, it is necessary for AD and AE to be equal, so they are arbitrarily given unit length here. It is clear that this forms a rigid structure, yielding only one solution for the dihedral angles. Actually, it is also possible to fold the faces downward and have them meet below, but that would simply be a reflection of what is seen here, so the solutions would be the same.

For this example, the dihedral angle at edge AB will be derived. Lay it back out into a flat net again. As the faces are folded, the vertex at point D revolves on axis AB and meets point P. This means that points D, P, and Q lie in a plane perpendicular to line AB. It follows that point Q lies on a line through D, perpendicular to AB. By the same reasoning, Q lies on a line through E, perpendicular to AC.

From right triangles ADF and AEG, it can be seen that AF = cosα, AG = cosγ, and FD = sinα. The immediate objective is to derive the measure FQ. For now, concentrate on quadrilateral AFQG. It has opposite right angles, making it a cyclic quadrilateral, so ∠Q = π - β.

In triangle AFG, use the law of cosines to solve for FG.

 

Now, find cos∠AGF.

 

Use the law of sines to find FQ.

 

Going back to the folded faces, we see that FP and FQ are both perpendicular to AB, so the angle labeled θ is the dihedral angle. From the right triangle PQF, we get this:

Other Cases

Certain other cases should be addressed. Up at the top, it is given that α and γ are acute. The first version of this derivation did not have that condition. Twelve years later, an alert reader pointed out that the substitutions AF = cosα and AG = cosγ were valid only for acute angles α and γ. Fortunately, the formula still holds up in spite of that lapse. In obtuse cases AF and AG may be taken as directed distances, with respect to AB and AC. Either of them may be negative or zero. The result is that FQ is a directed distance with respect to DQ. Where FQ is negative, the dihedral angle θ is obtuse.

Another issue arises in the middle. Although there is no problem with the final formula, some of the intermediate expressions may have division by zero. This occurs where one or more of the polygon angles are right angles. Such a case is not at all unusual where building polyhedra with regular polygon faces. Note that the final form of the formula involves a denominator that cannot possibly be zero. This case still must be proved separately (by someone else).

The formula applies only to cases in which exactly three faces meet at a vertex. There can be no general formula for a case in which more than three faces meet, because those faces by themselves would not form a rigid structure.

The Apothem, Polygon Area, and Surface Area

Given enough dimensions, it is possible to compute the area of any polygon, because the polygon can be dissected into triangles and the elementary triangle area formula can then be applied. For any regular polygon, the area can be computed from the side length alone.

Consider the regular polygon below, having side length s. It is a heptagon (having 7 sides), but since we want to derive a general formula, let us call it an n-gon (having n sides). By drawing radials from the center to each vertex, the n-gon is dissected into n congruent isosceles triangles. Now draw radials from the center to the midpoint of each side. This cuts the n-gon into 2n congruent right triangles.

Take out one of the right triangles (the yellow one) and look at it closely. Its base is s/2. The measure of the top vertex angle is π/n because it is a full circle divided by 2n. The height is a. This is the apothem of the n-gon. The apothem of a regular polygon is the distance from center to the midpoint of a side. It is also the radius of an inscribed circle. We can find the apothem from the side length and the number of sides.

 

That gives us the height of the right triangle, which leads us to its area.

 

There are 2n of those triangles in the n-gon.

 

For a Platonic solid, all of the faces are congruent regular n-gons. To get the total surface area (A), multiply the area of the n-gon by f, the number of faces.

 

Inradius and Circumradius

The inradius of a solid is the radius of the inscribed sphere. All platonic solids have an inscribed sphere. Other polyhedra generally do not.

In these illustrations, the solid being used is a dodecahedron, but the concepts and the formulas apply to all Platonic solids. Consider triangle OTM. Point O is the center of the solid. Point T is the center of the base, which is also the point where the inscribed sphere is tangent to that face. Point M is the midpoint of one of the base edges.

It is clear that line segment OM bisects a dihedral angle, so ∠OMT = θ/2, one-half of a dihedral angle. It should also be clear that ∠OTM is a right angle. These last two statements follow from the symmetry of the solid. What we have now is a right triangle with one know side and one known acute angle. A formula for the inradius, ri, follows.

 

The circumradius is the radius of the circumscribed sphere. It is the distance from the center to a vertex. All platonic solids have a circumradius. Continuing with the same dodecahedron example, let point U be a vertex on the same edge that point M occupies. The circumradius is OU. Points O and U are also opposite vertices of the rectangular prism shown here.

 

Volume

For a general formula for the volume of a Platonic solid, picture a pyramid built on one face, with the center of the Platonic solid as the apex of the pyramid. For the volume of the pyramid, we need its base area and height. Both of those values have already been computed. The base area is the area of a single face of the Platonic solid, and the height is the inradius of the Platonic solid.

 

In the same way, a pyramid can be built on every face. The pyramids would be congruent, and together, they would fill the solid. For the total volume (V), multiply the pyramid volume by f, the number of faces in the Platonic solid.

 

In this simplified formula, the volume is expressed in terms of the surface area and inradius.

Back to the Platonic Solids

Last update: January 21, 2016 ... Paul Kunkel whistling@whistleralley.com
For email to reach me, the word geometry must appear in the body of the message.