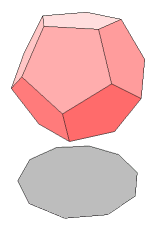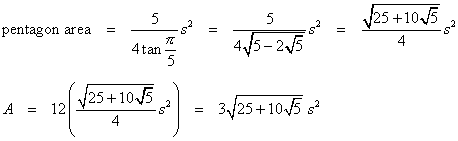
The dodecahedron has 12 regular pentagonal faces, 20 vertices, and 30 edges. Three faces meet at each vertex.
The pentagonal faces of this solid are a bit more difficult to deal with than the others. Follow this link for an explanation of some useful properties of the regular pentagon: Pentagon Properties
The calculations below are for a dodecahedron of side length s. Find the area of one face, and multiply that by the number of faces for the total surface area.
|
|
Three pentagons meet at each vertex, so the dihedral angle formula can be used with
|
|
Next, the apothem, the inradius, and the circumradius.
|
|
Finally, the volume.
|
|
The dodecahedron has 120 symmetries.
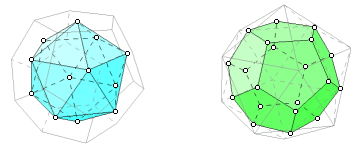
The dodecahedron is the dual of the icosahedron. Connecting the centers of adjacent faces of the dodecahedron results in an icosahedron, and connecting the centers of the icosahedron faces results in a dodecahedron.
By connecting select vertices of the dodecahedron, it is possible to form a tetrahedron or a cube. By connecting midpoints of certain edges, it is possible to form an octahedron.
|
|
|
|
A cross-section of the dodecahedron can be an equilateral triangle, a square, a regular pentagon, a regular hexagon (two ways), or a regular decagon.
|
|
|
|
|
|
|
|
The planar projection of a dodecahedron can be a regular decagon.