The Tetrahedron

The tetrahedron has 4 faces, 4 vertices, and 6 edges. Each face is an equilateral triangle. Three faces meet at each vertex.

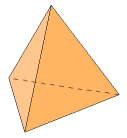
Begin with a tetrahedron of edge length s. Its faces are equilateral triangles. The length of their sides is s, and the measure of their interior angles is π/3.

First, find the area of each triangular face. Multiply that by the number of faces to get the total surface area, A.

The dihedral angle formula can be applied here because three faces meet at each vertex. All of the faces are equilateral triangles, so let α = β = γ = π/3.

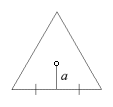
Find the apothem of a face, and use it in the calculations for the inradius and circumradius.

Now, the volume formula.

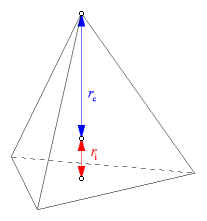
Here is another way to work out the volume. The tetrahedron is also a pyramid, and its height is the sum of the inradius and the circumradius. Use that fact and apply the pyramid volume formula. Redundant calculations like this are a good way of checking the results.

Other Properties

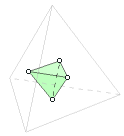
The tetrahedron is its own dual, meaning that if the centers of the adjacent faces are connected with line segments, the resulting figure is another tetrahedron. The smaller tetrahedron shown here has one-ninth the volume of the larger one, but it is not possible to assemble nine tetrahedrons into one.

The tetrahedron has 24 symmetries.

Tetrahedra do not pack space, but it is possible to pack space by combining tetrahedra and octahedra. This property is explained in more depth on the octahedron page.

The tetrahedron has no parallel faces, no parallel edges, and no diametrically opposite vertices. All of these properties are unique among the Platonic solids.

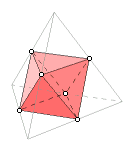
When the midpoints of the adjacent edges of a tetrahedron are connected, an octahedron is formed.

A cross-section of a tetrahedron can be an equilateral triangle or a square.

A planar projection of a tetrahedron can be an equilateral triangle or a square.

Back to the Platonic Solids