Conics of Apollonius

While reading a translation of Conics, by Apollonius, I found it helpful to construct many of the figures using The Geometer’s Sketchpad. I have decided to go ahead and do them all.

The books of Conics (Geometer’s Sketchpad documents)

These models in these Sketchpad documents are based on the following sources, used by permission:

Book I
Book II
Book III
Book IV
Book V
Book VI
Book VII

Sources

Conics Books I-III, translation by R. Catesby Taliaferro, diagrams by William H. Donahoe, Green Lion Press, 2000
Conics Books IV, translation and diagrams by Michael N. Fried, Green Lion Press, 2002
Conics Books V to VII, translation by G. J. Toomer, Springer-Verlag, 1990
Conics Books I to VII, translation and notes by Boris Rosenfeld

To my knowledge, the translation of Boris Rosenfeld was not published in book form. It includes all seven extant books and some very useful notes and analysis. This version has no diagrams, but it refers to diagrams found in other publications. Books I through IV are aligned with much earlier translations by Johan Ludvig Heiberg and Euangelos Stamatis. Books V through VII refer to the diagrams that were used in the Toomer translation. Svetlana Katok, Rosenfeld's daughter, has graciously made the translation available for download.

Translation
Translator’s commentary

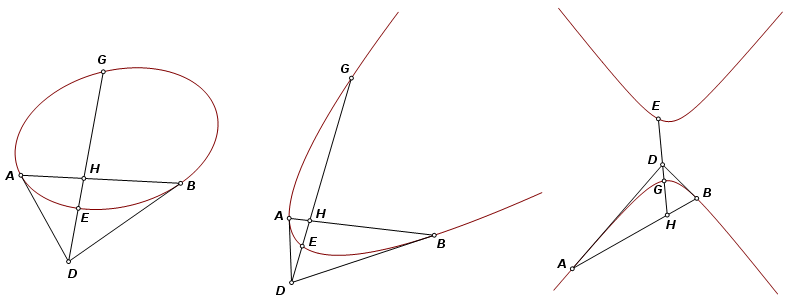
Apollonius

Apollonius of Perga lived in the third and second centuries BC. He is believed to have been born in about 240 BC. Among his great works was the eight-volume Conics. Our knowledge of many of his contemporaries is limited to little beyond vague conjecture or inflated stories that challenge credulity. Apollonius, at least on the subject of conics, can still speak for himself. The first four books of Conics have survived in the original Greek. Books V through VII survived thanks to the efforts of a ninth century AD family of scholars who stepped forward to translate and preserve them in Arabic. All seven surviving books are now available in English.

It is a sad fact that so many works of that era are lost and will never be recovered. There were frequent waves of political turmoil and war, which could wipe out entire civilizations, making the survival of a library unlikely. Also, consider that this was before the development of the printing press. Some of the books of Conics are preceded with personal notes from Apollonius in which he exchanges pleasantries with the recipient. It becomes apparent that he was personally transcribing entire books. Even when they were new they could not have been widely distributed, certainly not by modern standards.

This is not the first great study of conic sections. Euclid, who preceded Apollonius by about two generations, produced a four-volume work on the subject, but it has not survived. The first three books of Apollonius’s Conics may be largely a retelling of Euclid’s.

Books I-III

Books I through III were translated by R. Catesby Taliaferro of Saint John’s College in the 1930s, and were published more recently by Green Lion Press. Each book has 50 to 60 propositions, most of which are theorems. With few exceptions, the theorems are proved, sometimes with hand-waving “it is evident” statements, but the proofs are generally quite rigorous.

Certain other propositions are constructions, in which the author takes great pains to address every special case. In II.49, For example, the challenge is to construct a straight line through a given point and tangent to a given conic section. Apollonius justifies the construction for eleven special cases, and proves the nonexistence of a solution for one other case.

Naturally Book I has most of the definitions. The Apollonius model of conic sections includes oblique cones. It also uses conic surfaces of two nappes. The two disjoint opposite sections are exposed, but they are not included together in the definition of a hyperbola, and are never referred to as a single section. Conjugate opposite sections and the upright side (latus rectum) are given prominence. Points of application (foci) do not appear until Book III, and the directrix is absent entirely.

Book IV

The source for Book IV is a translation by Michael N. Fried. It too is published by Green Lion Press, and as of 2013, they have made the first four books available under one cover. Book IV has been less widely distributed until recently. Mathematics historian Thomas Heath said dismissively of this volume, “Book IV is on the whole dull, and need not be noticed at length.” There are two main properties in the book. Special cases and exceptions are addressed perhaps to the point of tedium, making Mr. Heath's impatience understandable.

It begins with properties of poles and polars, which were introduced in Book III. These properties align with more familiar properties involving circles. Let D be a point outside a conic section. Let tangent lines from D touch the section at A and B. Also, let a secant line from D cut the section at E and G, and let DH divide EG harmonically. It is true then that points A, B, and H are collinear.

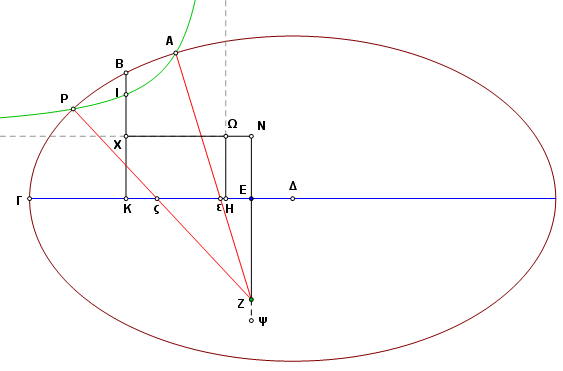
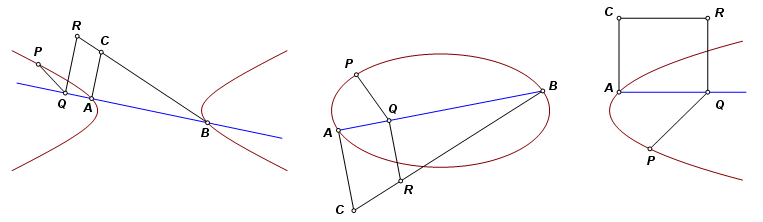
With the more widely accepted modern definitions, the only exceptions (more like special cases) would arise when D falls on an asymptote of a hyperbola, or when the cutting line DE is parallel to an asymptote. But what Apollonius calls a hyperbola is a single continuous curve. To him the double curve we now call a hyperbola is a pair of opposite sections, and is not classified as a single conic section. That means that Proposition 1, which purportedly applies to all conic sections, actually applies to a hyperbola only under specific conditions. A rather awkward result is that the first proposition must be qualified by subsequent propositions. Apollonius dutifully considers each of the special conditions, adds cases for opposite sections, considers the cases in which the exterior point falls on an asymptote, and considers cases in which the cutting line is parallel to an asymptote, hence Mr. Heath’s complaint.

The other major concept involves the number of contacts between two conic sections. They can meet at no more than four points. Again, special cases abound. When is the number of contacts fewer than four? Apollonius considers whether intersecting sections have concavity in the same direction or opposing directions, he considers tangency cases, and of course he addresses the many opposite section cases.

Many of the Book IV proofs are indirect proofs. They begin by assuming a geometric relationship that will ultimately be proved impossible. These models pose a problem for the Geometer’s Sketchpad, which will not draw the impossible. As a compromise, many of the proposition statements are illustrated with no direct connection to the figures in the proof. It should also by noted that some of the proofs are incomplete or flat-out wrong. Fried suggests that some of the text may have been corrupted in the 2200 years of transcriptions and translations. Unlikely as it seems, we must also acknowledge the possibility that Apollonius himself was mistaken.

Book V

The later books of Conics are handed down to us in a more indirect way. As they were not part of the core of conic section studies, the later books fell into disuse, and nearly disappeared entirely. The Banū Mūsā is the collective name for the three sons of Mūsā bin Shākir. The brothers were prominant scholars in Baghdad during the ninth century AD. They directed the collection and Arabic translation of the first seven books. Whether they ever acquired the eighth is unclear. In any case, it is now lost. The Banū Mūsā are the source of all subsequent versions of books V through VII, as the earlier Greek and Latin versions have been lost.

An excellent modern English translation of books V through VII was written in a two-volume set by G. J. Toomer (Springer-Verlag 1990). The first volume has historical background, analysis, and the translation itself. In the second volume are all of the diagrams and the translator’s notes. Anyone interested enough to purchase this set should be careful to seek out the original hardcover edition. There was a 2012 softcover edition which inexplicably includes Volume I only, not a single diagram.

Book V, to a large extent, concerns normal lines: whether they exist, how many exist, how they might be constructed. They are not actually called normals, although it is proved that each is perpendicular to the tangent line at the point where it meets the section. In most cases a normal line is called a minimum line, sometimes a maximum line. These designations refer to the distance between a point where a normal meets the section and some certain given point, usually on the axis. See the definitions below.

An interesting construction technique also is introduced. In Book II Apollonius showed that he was comfortable with the concept of conic sections as given objects in a construction. For example, in II.49 a conic section and a point on its exterior are given. The section itself could not have been constructed under the usual restrictions, but with compass and straightedge it was possible to construct a tangent line through the given point. Here in Book V he has taken it a bit further. The image below is from V.52. Traditional construction methods are used to define parameters of a hyperbola, and the hyperbola is then used as a construction object, intersecting an ellipse at the endpoints of two minimum lines.

Apollonius could not have had access to any means of representing these curves precisely, and an exact construction is impossible even in theory. This same proposition has a geometric division step, which would be equivalent to duplicating a cube, yet another impossibility. The construction itself is not the objective. Of greater importance than drawing the curves, Apollonius has proved that they exist, that they intersect, and that the intersections have certain properties.

The images in the Book V Sketchpad document are aligned with the Toomer diagrams, much as the earlier documents were aligned with the Green Lion books. The point labels are now Greek characters, with no italics. In the previous books most of the sections were left with an oblique orientation in order to discourage any misleading sense of up or down. Most of the propositions of Book V, however, involve relationships with the axes. For that reason, nearly all of the sketches were parked with the axes horizontal and vertical, although they can still be turned by dragging the control points. Most of the Toomer diagrams show only half of a section, cut along an axis. That convention was not followed in the Sketchpad document.

Book VI

Book VI is the shortest of the surviving volumes, with 33 known propositions. Toomer notes some discontiniuties in the manuscript, which might suggest some missing propositions. The book begins with several new definitions. One word used extensively is translated as “equal” by both Toomer and Rosenfeld, but its usage is actually more consistent with “congruent” in modern English. The same word is used for both concepts. The volume deals primarily with equality or similarity of conic sections or segments, also symmetries of sections.

Proposition 6 states that if any part of a section can be fitted to a second section, then the sections are equal. Once the concept is proved and accepted, many of the later propositions become intuitively obvious. Even the smallest segment of a section is sufficient for defining the entire section. Two distinct sections can coincide only on a few (no more than four) discrete points, and not on any continuous segment. Many of the proposition conclusions again are negatives, making them difficult to illustrate. Several sketches make use of the five-point conic construction, which did not come from Apollonius.

The cone itself has been on hiatus since Book I, but now makes a return. The final eight propositions of Book VI are constructions involving the cone and cutting plane. Most of them apply specifically to a right cone.

Book VII

In VII.2 is the first mention of the homologue (see glossary). This is the only surviving work in which Apollonius used it, and since it is here translated from Arabic, we cannot be sure what he called it. Most of the first twenty propositions concern relationships between the homologue and other objects on the section. It might first appear that this abstruse dimension is to be the center of attention, but it soon becomes clear that the ground is being laid for something else.

Beginning with VII.21, and continuing to the end of the book, there are relationships between axes, diameters, their conjugates, their latera recta, and figures constructed on diameters. Sums, differences, and squares are considered. Where are they maximized or minimized? Under what conditions are they constant? Nearly all the proofs of these propositions rely on the homologues and the propositions from the first part of the book. The division points of the homologues (Ν and Ξ) also are used in the construction of diameters at which certain optimal conditions occur.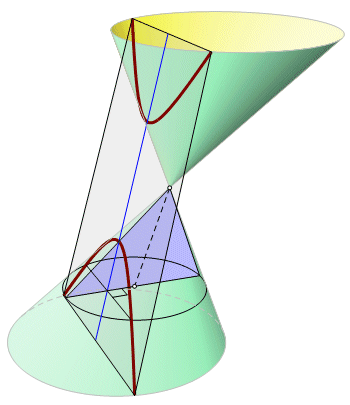

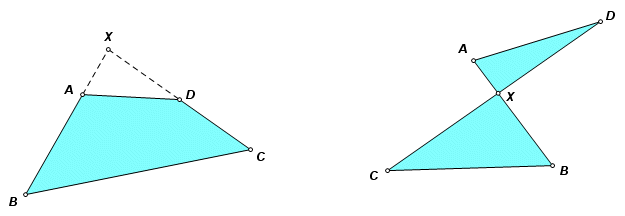
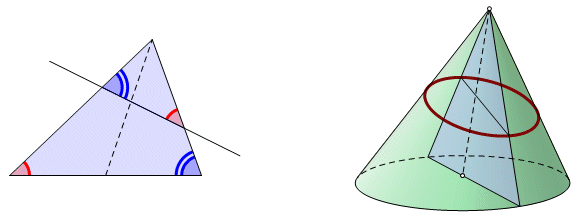
The Apollonius Model

Unlike his predecessors, Apollonius cut his sections from oblique cones. This presents us with a more general case, and a right cone is only a special case. An axial triangle is drawn in the cone. The cutting plane intersects the plane of the cone base at a line perpendicular to the base (or base produced) of the axial triangle. The section is the curve at which this cutting plane meets the conic surface. The cutting plane never goes through the vertex, so degenerate cases are not considered.

The intersection of the cutting plane and the axial triangle is a diameter. Early in Book I it is called the diameter. As the book progresses, it is made clear that for any section there are any number of other diameters.

The Circle as a Conic Section

Many of the propositions (e.g., II.29) require a section of a cone or circumference of a circle. This condition might suggest that Apollonius did not consider a circle to be a section of a cone. It is not clear why the circle was set aside. Excluding degenerates, any cutting plane parallel to the base of the cone will meet the cone at a circle. This cutting plane would not meet the plane of the base, and so would not fit the axial triangle model described above, but it is nonetheless a section of a cone. If the cutting plane lies subcontrariwise, it does meet the plane of the base, and the section is a circle.

In the Sketchpad constructions circle cases are omitted, except in those few propositions that address the circle alone. Otherwise the circle may be considered a special case of the ellipse having all of the properties of the ellipse.

The Sketches

Most of the original proposition statements are given in a single sentence, often a run-on sentence, which may cover half a page or more. I have left the simpler statements intact, just as the translator gave them, and they appear in quotation marks. For the more complicated statements I have rephrased them, stating conditions with calls to the labels in the sketch. In Book V, the proposition statements were so strung out that I ended up rephrasing all of them. Many of the sketches have measurements of distances, areas, or ratios, confirming the conclusion. None of the proofs are included here.

The sketches in the attached documents are generally consistent with those in my sources. With a few exceptions I used the same point labels so that this work could serve as a companion to the book. In a few cases it was useful to introduce other points. The proofs often require the introduction of many supporting constructed objects. These supporting objects are not always shown here, the primary emphasis being on the proposition statement. Some of the propositions also seem to be redundant, or have unnecessary exclusions. These may be followed by brief notes of my own.

The red points usually control the shape of a cone or conic section. Blue or green points are points on paths. Drag these to change the positions of tangents, diameters, and so on. White points are for reference, and are not intended to be used as controls. Diameters usually are drawn as blue lines, and asymptotes in red. These color conventions sometimes change for contrast.

Most of the pages have a button in the lower left corner labeled Show Controls. Click this to show the red points controlling the shape. There may also be a parameter labeled conic radius. The figures were found to be more manageable if parabolas and hyperbolas were not permitted to stretch out to infinity. This parameter controls how far the curves can go.

Many of the propositions have conclusions regarding the upright side, even if that side does not appear in the figure as a geometric object. Look along the left border of the screen, there may be a measurement labeled upright side.

There is some inconsistency with regard to representations of the latus rectum, which often appears in Book VII. It generally is drawn as a line segment attached to a vertex of its corresponding diameter. Its direction, however, may be tangent to the section, perpendicular to the axis, or perpendicular to the corresponding diameter, as a side of the figure constructed on that diameter. There is no geometric necessity for any of these positions. In fact, the source sketches often had the latus rectum separated entirely from the rest of the figure. There was some attempt to align the images with those in the figures of the translation sources. There was also a need to avoid cluttering the sketch.

Book I has quite a number of spatial representations, which is why that document is so much larger than the others. These figures can be tilted and turned. The best way to learn is by experimenting with the controls. Bear in mind that these are merely projections of solids and surfaces. Sketchpad is strictly two-dimensional. Measuring the distance between two points on a perspective sketch will render the distance between the projections, not the correct distance between the points. Some of these sketches have calculated distances, based on the controlling objects. These may be regarded as true values.

Self-intersecting Quadrilaterals

Beginning in Book III there are several propositions that make conclusions concerning the difference of two triangles, where the triangles have a common vertex and two pairs of collinear sides. Since the triangles are controlled by dynamic objects, it is not always possible to know which triangle will be bigger, or whether the triangles overlap.

Certain computer graphics programs, including Sketchpad, use a convention that simplifies this measurement. Start with quadrilateral ABCD. Now drag one of the vertices so that sides AB and CD intersect at point X. The quadrilateral capsizes into a self-intersecting quadrilateral, sometimes called an antiquadrilateral, or a bowtie. Its interior is now the interior if two triangles. Its area is taken as the difference in the areas of its triangle parts, always non-negative. Intentionally or not, this is exactly what was required. The difference of two triangles can therefore be expressed as the area of a single quadrilateral, which may or may not intersect itself.

Glossary of Terms

Conics has formal definitions for most of the important terms, but uses them somewhat inconsistently. In spite of this, the intended meaning is usually perfectly clear.

asymptote – This word was not exactly translated, since Apollonius used the same word. In his day it could have a different meaning. An asymptote was a line that did not meet a given curve. Hence, it is sometimes suggested that a hyperbola can have more than two asymptotes. So it appears in II.1 and II.14. After that the word aligns with the modern English usage in which an asymptote is a line approached by a curve.

axial triangle – Let the endpoints of a diameter of the base of a cone joined to the vertex by straight line segments. The resulting triangle includes the axis of the cone, and is called an axial triangle. There are several references to the two sides of an axial triangle. This refers to the sides on the conic surface, and the side on the base is excluded.

axis – A diameter of a section that bisects a set of parallel chords at right angles is an axis of the section. If conjugate diameters are also axes, then they are conjugate axes. Most of the early propositions of Conics address general cases, and the axis does not come up very often until Book V.

The straight line joining the vertex of a cone to the center of the base is the axis of the cone. In the case of an oblique cone, the axis is not an axis of rotation.

center – The midpoint of a diameter (or transverse side) of an ellipse, hyperbola, or opposite sections is the center. Since the hyperbola has only one branch, it has no center of symmetry, but the word is used freely with hyperbolas.

cone – A cone is the figure contained by the base, the conic surface, and the vertex. Unlike the conic surface, the cone is bounded. This definition would make the region a solid, but when a cutting plane makes a section, only its intersection with the lateral surface is considered, not the interior or the base.

conic surface – Begin with a circle (the base) and a point (the vertex) not in the plane of the circle. From the vertex a straight line is drawn to a point on the circumference of the base, and the line is produced in both directions. While holding the vertex fixed, let the point on the base travel through the circumference. The locus of the line is a conic surface. The straight line joining the vertex and the center of the base is the axis.

conjugate diameters – If each of two diameters bisects the straight lines parallel to the other, the diameters are conjugate diameters. This applies to a single curve (ellipse or circle) or two curves (opposite sections). This term is at odds with a prevalent modern English usage in which the upright axis of opposite sections is called the conjugate axis. With the definition given here, there can be no such thing as a single conjugate axis. There must be two, and they are conjugates of each other. This also would seem to be more consistent with other usages of the word “conjugate.”

conjugate opposite sections – This figure first appears in I.60. It is two pairs of opposite sections. The transverse side of each is the second diameter of the other. They have the same asymptotes.

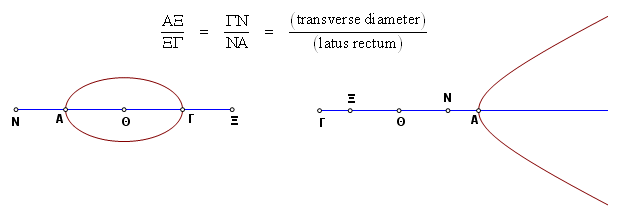
contain – A cone is said to contain a section if the section is entirely in the cone, in the conic surface produced at the base, or both. The definition does not allow for producing the conic surface at the vertex, so this would seem to apply to one nappe only.

diameter – Let a straight line have an endpoint on a curve and bisect all chords of the curve that are parallel to some given straight line. A line with this property is a diameter. A point where the diameter meets the curve is a vertex. Since the diameter does not have to meet the chords at right angles, it is not necessarily an axis. The word must be interpreted in context. It sometimes refers only to that part of the line within the curve, but sometimes it is the entire line produced. Still at other times it is the part between the vertices, although, in the case of a hyperbola or opposite sections, that specific line segment does not bisect any chords.

eidos – This is the term preferred by Rosenfeld for the figure of a section constructed on an axis or a diameter. See that definition below.

ellipse – Let the cutting plan cut both sides of the axial triangle. The section formed is an ellipse

equal sections – Two sections are equal if they can be fitted onto each other with neither exceeding the other. In modern English we would call the sections congruent, but it seems that Apollonius used the same word for equality and congruence. In fact, we often do that still with line segments and angles, but not with sections.

figure of a section constructed on an axis or a diameter – The figure (or eidos) is a rectangle. One side is a diameter (possibly an axis), and the other is the corresponding latus rectum. From this rectangle it becomes clear how upright side became another term for the latus rectum. Although the figure is used even in Book I, it is not properly defined until the introduction to Book VI. The square on the conjugate axis is equal to this figure in area.

homologue – Let ΑΓ be an axis of an ellipse or hyperbola. Let ΑΓ be divided by points Ξ and Ν (externally in the case of the ellipse, internally in the case of the hyperbola) in the following ratio:

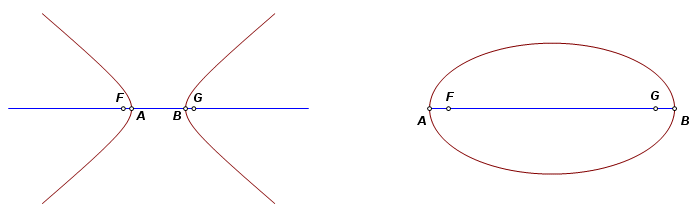
Line segments ΑΝ and ΓΞ are homologues. A parabola, having only one vertex, has no homologue. As an ellipse approaches the form of a circle, the division points Ν and Ξ are flung toward a point at infinity. In Book VII these line segments are used extensively, and Apollonius, or his translators, quite consistently used the same five point labels that appear above.

hyperbola – Let the cutting plane cut the axial triangle in such a way that it cuts one side produced on the opposite side of the vertex. The resulting section on one nappe of the conic surface is a hyperbola.

It was Apollonius who first introduced the word hyperbola. His hyperbola consistently has only one branch. It is a single continuous curve. Although it has only one branch, there are numerous references to a hyperbola having a center, two vertices, and two points of application, just as though the second branch were there.

latus rectum – See upright side. This is simply a difference in the translation. Toomer and Rosenfeld both used this term, so it was adopted for the Sketchpad documents, beginning with Book V.

maximum line – From a point on the minor axis of an ellipse, of the lines drawn to the section, the one with the maximum length is the maximum line. It is normal to the section, but it is not called by that name. The ellipse is the only conic section having a maximum line. See also minimum line.

minimum line – From a point on an axis of a conic section, of the lines drawn to the section, the one with the minimum length is the minimum line. It is normal to the section, but it is not called by that name. It sometimes is called simply a minimum. The definition also may be used loosely, referring not only to the line segment cut off by the section and its axis, but also to the line containing that line segment. See also maximum line.

oblique cone – If the axis of a cone is not perpendicular to the base, it is an oblique cone. Unlike his notable predecessors, Apollonius stated of his theorems in the most general terms, applying to an oblique cone.

opposite sections – Let the cutting plane cut the axial triangle as it does with the hyperbola. It cuts one side produced on the opposite side of the vertex. It meets the conic surface at two opposite sections, one on each nappe.

Today a hyperbola is generally regarded as a single curve of two parts. To Apollonius these branches were opposite sections. He showed that each branch was a hyperbola, but he never referred to them together as one hyperbola. Regarding opposite sections, there occasionally is ambiguity in the given conditions. E.g., if two tangents touch opposite sections, is it allowable for the points of contact to be on the same section? That is not always clear.

parabola – Let the cutting plane cut the base and one side of the axial triangle, and let the other side be parallel to the plane of the cutting plane. The section formed is a parabola

placed in a cone – A section is placed in a cone if the cone contains the section. See contain.

points of application – These are now called foci. In Conics, they make their first appearance in III.45. Applied to any ellipse, circle, hyperbola, or opposite sections, the points lie on an axis. On each side, a rectangle equal to the fourth part of the square on the figure is applied to the axis, which algebraically means this:

In the case of a hyperbola or opposite sections, the rectangle is exceeding by a square figure. For an ellipse, it is deficient. This means that the points fall outside of the vertices in the former case, and between them in the latter. It is not stated, but the conditions would require the major axis for the ellipse case. For hyperbolas and opposite sections, the transverse axis is implied, but not stated. A circle has any number of axes, all having the same single point of application, the center. The axis of a parabola, having no finite length, has no point of application fitting this definition. Strangely enough, Apollonius did not address the parabola focus. In fact, he gave only cursory attention to the foci, and none at all to directrices.

right cone – A cone having its axis perpendicular to the base is a right cone. The right cone may be considered a special case of the more general oblique cone. With few exceptions (see the subcontrary section), it has all of the properties of the oblique cone.

second diameter – The expression “first diameter” is never used, but the first diameter identified is often called the transverse diameter. The second diameter is a straight line, is bisected by the center, is parallel to an ordinate, and is a mean proportion of the sides of the figure. That last condition indicates that it is the geometric mean of the transverse side and the upright side. This gives the second diameter finite length. In the case of an ellipse, its endpoints are on the section. For a hyperbola or opposite section, the second diameter does not meet the section, even when produced. The parabola, having no transverse side or center, cannot have a second diameter.

This is another term that must be taken in context. It sometimes refers to the line produced.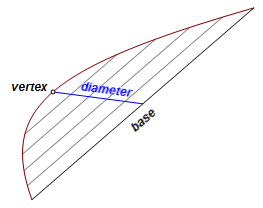

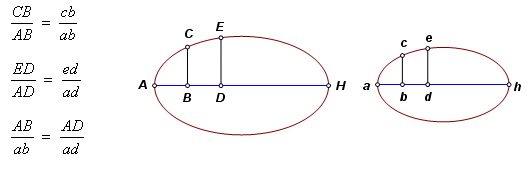
segment – A segment of a circle or conic section has parts which mostly correspond to the segment as a whole. The base is the line which subtends the segment. The diameter is the line which bisects all lines drawn across the segment parallel to the base. The diameter meets the segment at the vertex of the segment.

Segments are equal from their bases up if they can be fitted onto each other with neither segment exceeding the other. Segments lacking this property are unequal. See the entry on equal sections. In modern English usage these equal sections normally would be called congruent.

similar right cones – Right cones are similar if the ratios of the axes to the diameters are equal.

similar sections – Similarity of sections means just what we would expect. At the beginning of Book VI it is given this rigorous test. Let two sections have corresponding axes AH and ah. The sections are similar if for any ordinates CB and ED in the first section, there exist corresponding ordinates cb and ed in the second satisfying these proportions:

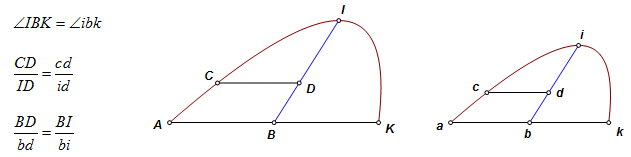
similar segments – Similar segments do not generally have axes, so the definition involves proportions on an oblique diameter. Let segments have corresponding bases AB and ab, and diameters IB and ib. The sections are similar if for any ordinate CD on the first segment, there exists a corresponding cd on the second, and these relationships are satisfied:

subcontrary – In I.5 the subcontrary section is described. The cone must be oblique. The axial triangle must be perpendicular to the base of the cone, which makes it also the plane of symmetry. Now let the cutting plane not be parallel to the base, but cut a similar triangle from the axial triangle. The cutting plane is then said to lie subcontrariwise, and the section is a circle. In I.9 it is proved that the section is a circle only if the cutting plane is parallel to the base or subcontrariwise.

transverse diameter – Let there be two curves. A straight line meets both curves and bisects all chords of either curve parallel to a certain straight line. This is a transverse diameter. A point where the transverse diameter meets either curve is a vertex.

There is inconsistency in the usage of this term. The definition given by Apollonius requires two curves, which would apply only to opposite sections, but the term used freely with all classes of conic sections.

transverse side – This refers specifically to that part of a given diameter lying between the vertices. This can be confusing. Take it in context. The transverse diameter and transverse side usually refer to the diameter that is first identified.

upright diameter – Let there be two curves. A straight line lies between the curves and bisects all lines intercepting both curves and drawn parallel to some straight line. This is an upright diameter.

In III.27, on an ellipse, the conjugate of a given diameter is called the upright diameter. That description would be more consistent with the second diameter, and, in fact, an ellipse cannot have an upright diameter as defined above.

upright side – This is an important concept, and is used often in Conics. The upright side is also occasionally called the parameter. In certain other works it is called the orthia, and it is equivalent to the latus rectum in modern usage. It is often represented as a line segment. It also appears as a magnitude to complete a ratio. Book I has several constructions for the upright side.

The upright side is used as shown here to demonstrate a relationship between the abscissa and ordinate of a point on a conic section. See below.

In all three cases above, the blue line is the diameter, point A is a vertex, AC is the upright side, and from point P on the the section an ordinate is dropped to Q on the diameter. In the opposite sections and the ellipse, straight line BC is drawn, where B is the other vertex. In the parabola case there is no second vertex, so a line is drawn from C parallel to the diameter. From Q a line is drawn parallel to the upright side, meeting the previously mentioned line at R. This relationship results:

PQ² = (AQ)(QR)

In figures such as these the upright side usually is drawn perpendicular to the diameter or perpendicular to the plane of the section. Its orientation, however, matters only to the extent that it cannot be in line with the diameter. In I.11-13, the upright side is constructed from a cone, an axial triangle, and a cutting plane.

Back to Conics

Back to Whistler Alley Mathematics