Conic Sections and Constructions

Mathematics curricula are ever changing to meet changing needs. In order to make room for new subjects it becomes necessary to downsize others. One subject that has received the short shrift is the study of conic sections. I have no strong opinions about the judgment of this change, but I do regret the loss. This is such a fascinating study, and it appeals to so many levels.

My original intention for this article was to show some constructions related to conics. The constructions are still here, but I decided that they should be supported by an explanation of some of the conic properties that were used. As it turned out, the conics defied all of my attempts at a concise summary, so I have the more expanded version below. As in the Greek tradition, my interest lies mainly in the geometric properties, so analytic models are omitted, at least for now.

Conic Constructions – This is a collection of constructions with conics. Some of them define a conic section locus given certain parameters. Others have the section as a given object from which certain points and lines are constructed.

The Conics of Apollonius – Near the year 200 BC, Apollonius of Perga produced an eight-volume treatise on conics. Most of it still survives. Here are dynamic Geometer’s Sketchpad constructions illustrating each proposition of that work.

Contents of this reference page:

Surface Intersections
Abscissa/Ordinate Model
Tangent Properties
Focus/Directrix Model
Two-Focus Model
Pascal’s Theorem
Transformation of Conics
Recommended Reading

Web Sketchpad (the red points)

Watch for the sketches that have red points. Those are dynamic geometry images. The developers of The Geometer’s Sketchpad have been working to make Sketchpad documents that can be viewed on a web browser. Several of them are among the images below. The images can be manipulated by dragging the red points.

Release: 2015Q2-1, Semantic Version: 4.2.1, Build Number: 911.7-r, Build Stamp: dn.kcptech.com/20150724142440

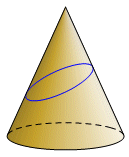
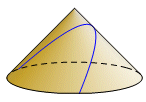
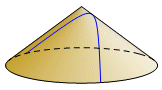
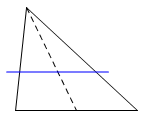
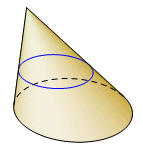
Surface Intersections

Conic sections are planar curves, but they derive their name from a spatial model. The curve can be the intersection of a cone and a plane. There have been different variations on that model following different notions of what a cone is.

When Archimedes mentioned a cone, he was usually (not always) referring to a right circular cone. Begin with a circle. A line through the center and normal to the plane of the circle is the axis. Somewhere on the axis is the vertex. Generators are the line segments connecting each point of the circle with the vertex. Together the generators form the lateral surface of the cone. The base may or may not be considered part of the surface.

Now, still using the Archimedes model, a plane is drawn normal to one of the generators. The intersection of the plane and the surface of the cone is a conic section. The class of the conic section depends on the vertex angle.

ellipse acute vertex angle	parabola right vertex angle	hyperbola obtuse vertex angle

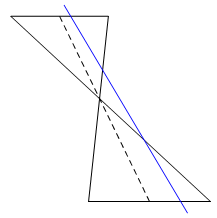
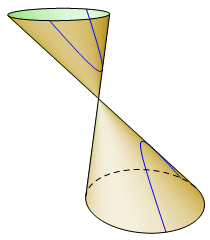
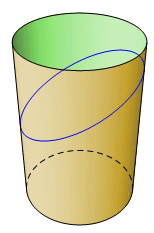
This particular model cannot be used with all conic sections. For example, a circle cannot be modeled this way. Apollonius of Perga preferred an oblique cone, and the intersecting plane did not have to be perpendicular to any of the generators. Eventually, it became common to use a cone with two nappes. This fits particularly well with a hyperbola, which can be represented as a curve with two separate parts. A cylinder might even be used in place of the cone.

circle oblique cone cut by plane parallel to base	hyperbola oblique cone with two nappes	ellipse cylinder cut by oblique plane

If we count the degenerate forms, there are quite a number of different classes of conic sections. None of the models above will cover all of them. Here is a list:

circle, ellipse, parabola, hyperbola, two intersecting lines, two parallel lines, one line, one point

Abscissa/Ordinate Model

The conic section was perhaps discovered by Menaechmus in the fourth century BC. A large body of conic theorems was produced by Aristaeus, Euclid, Archimedes, and Apollonius. They did not have coordinate geometry in the form that we now use, but they did have a related abscissa/ordinate system that worked well for describing properties of conic sections in the plane. The abscissa is the distance measured along a diameter from a vertex. The diameter used is not necessarily an axis of symmetry. The ordinate is the distance that the curve is offset from that point. The ordinate direction is parallel to the line of tangency at the vertex.

Any diameter of an ellipse must include the center. In the ellipse below, let AB be a diameter, let O be the center, and let P be a point on the ellipse. Point P is projected onto the diameter in the ordinate direction at point C. The abscissa of P is AP or BP. As P moves along the curve, the following relationship holds true. The first form is known as the two-abscissa form. The second form is equivalent. The ratio is constant over all points P on the curve aside from the vertices themselves.

The image below is dynamic. Drag the red points to see the relationships.

In the first case, the ordinate direction is orthogonal to the diameter, and the diameter is an axis of symmetry. In fact, that is not necessary. Ellipses and other conics also have oblique symmetry. Drag point A to a different position. The ordinate direction will be parallel to the tangent line at A. The ratio has now changed, but it is still constant as P moves along the curve. In the first case, there is reflection symmetry on the diameter, also called orthogonal symmetry. In the second case, there is oblique symmetry. In either case, every chord parallel to the tangent at A is bisected by diameter AB.

An equivalent relationship holds true for the hyperbola. In fact, the two-abscissa form is unchanged. The central form requires some rearrangement because OC is greater than the radius. The constant ratio also has a connection with the asymptotes. Point Q on an asymptote is projected ordinatewise to point R on the diameter. These three ratios are equal and constant over all points P on the curve other than the vertices, and all points Q on the asymptotes other than the center.

In dynamic image below, these relationships can be verified by dragging the red points.

The parabola is another matter. For one thing, a parabola has no center. Every diameter is parallel to the axis of symmetry. Each diameter has only one vertex, so the above ratios have no meaning. In this case, the abscissa is measured from A, the vertex, and the square of the ordinate is in constant ratio with the abscissa. Again, there is oblique symmetry.

Drag the red points to see the relationships.

Tangent Properties

Continuing with the abscissa/ordinate model, let P be a point on an ellipse. Again, let it be projected ordinatewise onto the diameter at point C. Also, let the line tangent to the curve at P intersect the diameter at S. Points C and S divide the diameter AB harmonically.

The relationship holds up whether the symmetry is orthogonal or oblique.

Drag the red points to see the relationships.

Let corresponding points be defined on a hyperbola. Also, let the line of tangency intersect the asymptotes at points U and V. The harmonic division is still true, and P is the midpoint of UV.

and UP = PV

Drag the red points to see the relationships.

In order to understand how this relates to the tangency properties of a parabola, it helps to write the proportion in another form.

A parabola may be imagined as an ellipse or hyperbola in which one vertex has been cast out to infinity. Let that be vertex B. As B approaches infinity, the ratio on the right hand side approaches one, which means that AC and AS approach equality. In the case of a parabola, they are in fact equal.

AC = AS

Drag the red points to see the relationships.

Focus/Directrix Model

Many of the ancient works mentioned above are now lost, but in the third or second century BC, Apollonius produced an eight-volume work, Conics, most of which still survives. The focus is mentioned only briefly, and the directrix not at all. We do not know with certainty whether the concept was even known in that era. And if it was not, then when did it arise?

The focus of a conic is a fixed point, and the directrix is a fixed line. A point moves on such a locus that its distance to the focus and its distance to the directrix are in constant ratio. Under those conditions the locus is a conic section. In the illustrations below point F is the focus, point P is the moving point, and point Q is the projection of P onto the directrix. The ratio PF : PQ is the eccentricity of the curve. The class of the curve depends on the eccentricity.

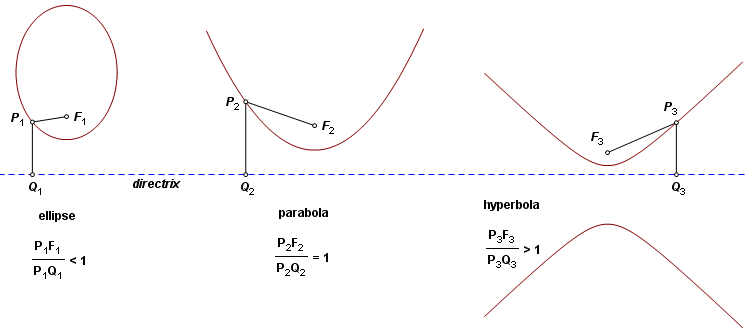
0 < PF : PQ < 1	ellipse
PF : PQ = 1	parabola
1 < PF : PQ	hyperbola

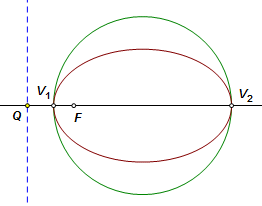
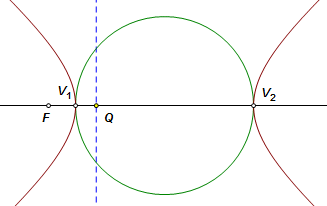
Certain degenerate cases can be defined with this model by letting the focus lie on the directrix or by making the eccentricity zero. The circle, however, will not fit well even as a limiting case. We might try moving the directrix to a line at infinity and put the focus at the circle center. Every point on the circle would return a constant ratio of zero. Unfortunately though, so would every other point in the plane. A circle cannot be defined with this model.

Consider an ellipse or hyperbola with vertices V₁ and V₂. Let F be a focus, and let Q be the point where the focal axis intersects the directrix corresponding to F. The eccentricity, e, may be expressed by either of these ratios:

This proportion also means that the ellipse (or hyperbola) divides the line segment FQ harmonically in ratio e. Stated another way, points F and Q are inversion images of each other in the circle having diameter V₁V₂.

Two-Focus Model

The ellipse and the hyperbola each have a second axis of symmetry. The focus and directrix may be reflected across the second axis, resulting in another focus-directrix pair, which can be used to define the same curve. We can also disregard the directrices and work only with the foci. Here are some useful properties.

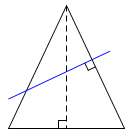
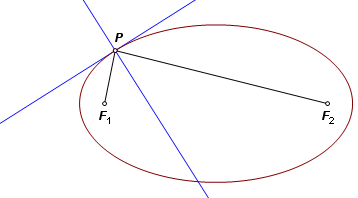
Let F₁ and F₂ be the foci of an ellipse, and let P be a moving point on the curve.

The sum of the distances PF₁ and PF₂ is constant.

The internal bisector of ∠F₁PF₂ is normal to the curve.

The external bisector of ∠F₁PF₂ is tangent to the curve.

A circle is a limiting case of an ellipse where the foci are coincident. In that case the single focus is the center of the circle.

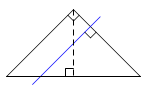
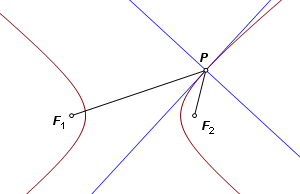
Let F₁ and F₂ be the foci of a hyperbola, and let P be a moving point on the curve.

The difference of the distances PF₁ and PF₂ is constant.

The internal bisector of ∠F₁PF₂ is tangent to the curve.

The external bisector of ∠F₁PF₂ is normal to the curve.

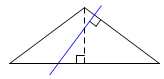
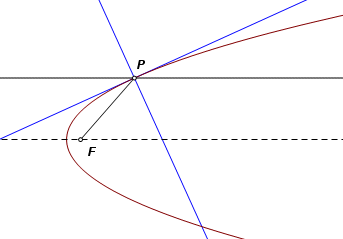
The parabola is again somewhat troublesome, this time because it has no second focus. Still it may be viewed as a limiting case of either the ellipse or the hyperbola. Start with either of these curves, and send the second focus to a point at infinity in the direction of the axis. Now it is a parabola.

Construct two lines through P, one through the focus and the other parallel to the axis. Bisect their angle of intersection. One bisector is normal to the curve. The other is tangent.

Pascal’s Theorem

It is said that Blaise Pascal discovered this property at age sixteen. He was a brilliant man who lived a short life, so we should be pleased that he began at such an early age. His theorem is included here in appreciation of its beauty and in order to support some of the constructions.

Let a hexagon be inscribed in a conic section. Here hexagon may be interpreted as lines connecting six points in sequence. The lines do not end at the vertices, and they may intersect each other at other points. Excepting parallel cases, there are three points at the intersections of opposite sides. These three points are collinear.

This property is shared by all conic sections on which it is possible to inscribe the hexagon. That includes all of the curved sections and the degenerate cases of two lines.

Drag the red points to see the relationships.

Transformation of Conics

The isometric transformations include translation, reflection, rotation, and any combination of these. By definition, these transformations preserve distance, and because of that, they also preserve angles. Under an isometric transformation, the image of any figure is congruent to the pre‑image. Dilation is not isometric. It does not preserve distances, but it does preserve ratios of distances, hence angles. Under dilation, images are similar to their pre‑images. Under any of the above transformations, a conic can only be transformed to another conic.

The really interesting property comes under two other transformations, one-dimensional scaling and shear. These transformations do not preserve distances, ratios, or angles. Images generally are not similar to pre‑images. However, although ratios in general are not preserved, ratios of distances measured in parallel directions are preserved. Consider what this means for the ratios discussed in the abscissa/ordinate section. After transformation, they must still be constant. A conic section may change shape considerably under a scaling or shear transformation, but its image will still be a conic of the same class.

In the image below, an ellipse, a parabola, and a hyperbola are subjected to scaling and shear. Their common axis is the invariant line.

Drag the red points to see the relationships.

The foci and directrices are not shown here, because they do not retain their properties under the transformation.

When the asymptotes of the hyperbola are subjected to the same transformation, they remain asymptotic. Upon scaling, the invariant axis remains an axis, but under the shear it becomes an oblique diameter.

There is an interesting exception to the non‑similarity rule. The image of the parabola is similar to the pre‑image. In fact, all parabolas are similar.