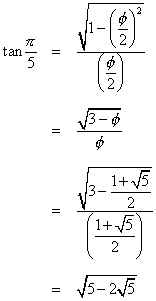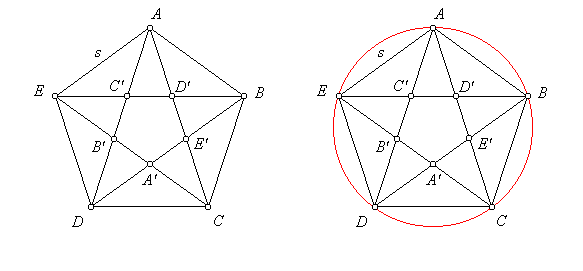
The regular pentagon is a deep file. Within it can be found self-similarities and repeated occurances of the golden ratio.
Begin with regular pentagon ABCDE, with side length s. By drawing the five diagonals of that figure, we can inscribe a star, commonly called a pentagram. Let A', B', C', D', and E' be the five points of intersection of the diagonals.

From the symmetry
of the figure, it is clear that C'AD' is an isosceles triangle. If
we circumscribe a circle about the pentagon, we see that
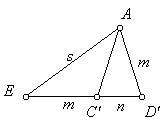 From the symmetry of the pentagram, EC' = AD'.
Let that length equal m, and let
From the symmetry of the pentagram, EC' = AD'.
Let that length equal m, and let
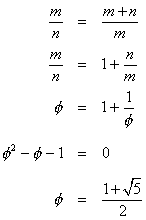
There is only one solution to the quadratic equation because, in this
case, we know that φ must be positive.
This ratio makes many appearances in the pentagon. Notice above that triangle
DAC is similar to triangle C'AD'. Therefore,
Now that we know the ratio of a diagonal to a side, that ratio can be used to evaluate several trigonometric functions of angles found in the pentagon. These values will be needed in later calculations. Consider a pentagon with unit side length. The measure of its diagonal must then be φ. Cut the pentagon at a diagonal to form triangle STU, as shown below. All of the sides and angles are known.
In calculations involving φ, it is often helpful to make use of the identity
For some of the dihedral angle calculations, it will be necessary to know cos(3π/5) and sin(3π/5). Use the law of cosines for this.
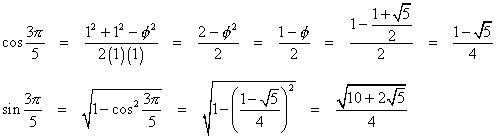
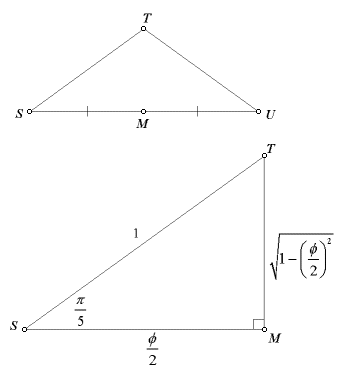
For the pentagon apothem, tan(π/5) will be needed. This calculation might be simplified by constructing the midpoint, M, of side SU. This results in right triangle SMT.