Tangent at a Point on the Curve

Construct a line of tangency through a given point on a conic section.

This one is very pleasing for its simplicity. We could make use of the focus properties, but it is not necessary to construct a focus or any other object related to the curve. In fact, the compass is not even required. This construction is completed with a straightedge only. First consider two background concepts.

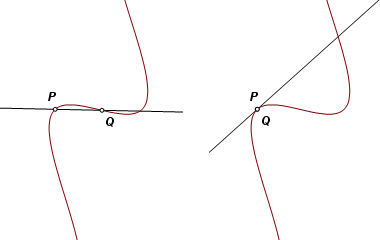
Let P be a fixed point on any differentiable curve, not necessarily a conic. Let Q be a traveling point on the same curve. As Q approaches P, the secant line PQ approaches tangency at P. This is an important concept in calculus. Of course when Q reaches P, there is only one point, so no line can be defined, which is one reason why calculus involves limits.

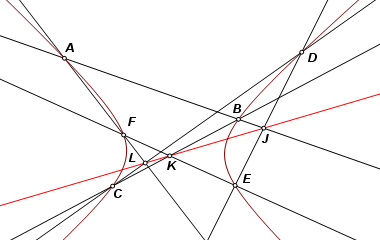
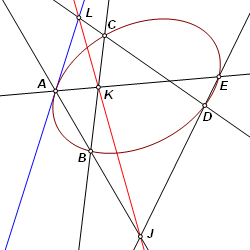
This illustrates Pascal’s theorem. Hexagon ABCDEF is inscribed in a conic (a hyperbola in the example). Opposite sides intersect as follows:

AB and DE at J
BC and EF at K
CD and FA at L

Points J, K, and L are collinear, as the red Pascal line shows.

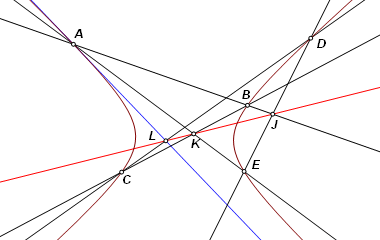
Now suppose that point F is moved toward A. Line AF will then approach tangency at A. There is still the problem of constructing line AF when A and F are coincident, right? But no, that is not really a problem at all. Line AF is not required for the construction of point L, which is the intersection of BC and the Pascal line, JK.

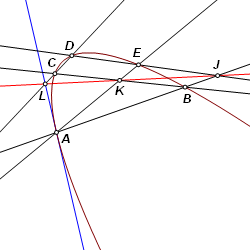
To construct a tangent line at A, inscribe pentagon ABCDE. Construct intersection points as follow:

AB and DE at J
BC and EA at K
CD and JK at L

The line of tangency can then be constructed as AL.

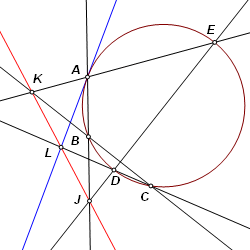
The same construction applies to all curved conic sections. It may require some maneuvering of the inscribed points in order to avoid having intersection points fall off the screen. For pencil and paper constructions, this may present the additional problem of weak intersections.

Back to Conic Constructions

Back to Whistler Alley Mathematics