The Five-Point Conic

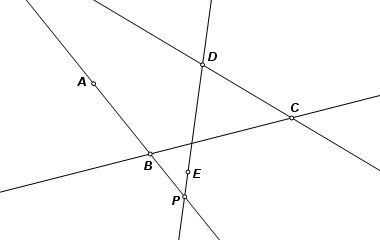
Given five points, construct the conic section that includes all of the given points.

The solution to this challenge lies with Pascal’s theorem. When a hexagon is inscribed in a conic, the three pairs of opposite sides define three points of intersection. These three points are collinear. In this application, five of the hexagon vertices are given. The conic section is the locus of the sixth vertex, which must satisfy the property of collinearity.

Let A, B, C, D, and E be the five given points. These define four sides of the hexagon. Sides AB and DE are the only opposite pair. Let them intersect at point P.

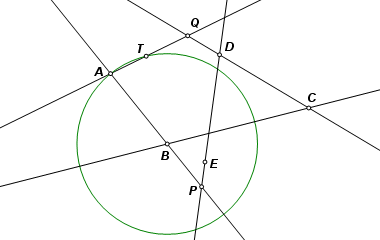
Construct a circle centered on B and passing through A. Point T is a traveling point on that circle. The center of the circle was an arbitrary choice, but it must go through A. Now as T follows its path, line AT turns through every possible orientation once.

Line AT is actually FA, with point F still unknown. It intersects opposite side CD at point Q.

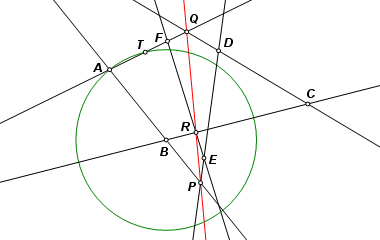
With points P and Q, we can define the Pascal line, shown here in red. Side BC intersects it at point R. Lines BC, EF and the Pascal line must be concurrent, so F must lie on ER. Point F is the intersection of ER and AT.

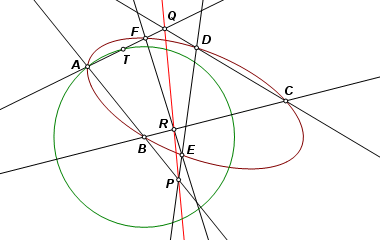
As T traverses its circular path, point F remains on the conic, and its locus is the entire conic section.

The completed construction.

If your browser has Java enabled, drag the points to view other cases.

Back to Conic Constructions

Back to Whistler Alley Mathematics