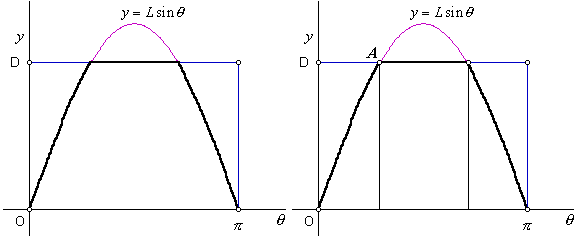
My presentation of Buffon’s Needle was placed on the web in 1997. Since then, several visitors asked for a derivation of the formula for the case in which D < L. It follows the same line of reasoning as the other case. The outcome of a trial may be modeled with θ-y coordinates of a point. All possible outcomes fall within the rectangle shown here, with 0 < θ ≤ π and 0 < y ≤ D. If the point falls beneath the curve y = Lsinθ, then the outcome is a success. This time, we cannot simply use the area of the region beneath the curve, because, when D < L, not all of the curve is on the rectangle’s interior. We need the area of the region that is both beneath the curve and within the rectangle. In the second drawing, that region is divided into three parts.
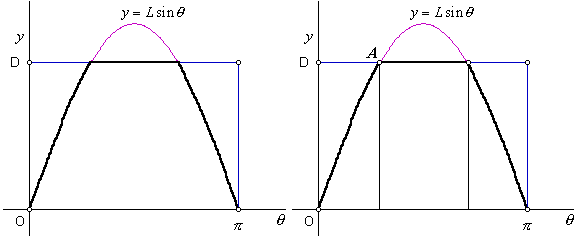
|
Let’s first get the area of the rectangular region in the middle. Point A is the first intersection of the curve and the top of the rectangle. We will need the coordinates of point A. Clearly its y-coordinate is D. So, substitute that into the curve equation, and solve for θ.
|
|
The width of that red rectangle is π minus two times the θ-coordinate of point A. Its height is D. So, this is the area of the red rectangle:
![]()
|
Now find the area of the other two regions. They are congruent, so we will derive the area of the left one, and double it. Its top boundary is the curve, and we know its left and right limits. The area can be found by integrating. |
|
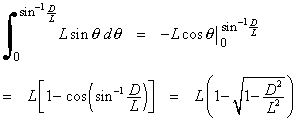
We can get away with that last substitution because the angle is in the first quadrant, so the cosine is positive. Now double this area, and add it to the rectangle area calculated above. The sum is the total area for the region representing successful outcomes.
|
Area of success region.
|
|
|
For the probability, that last area must be divided by the area of the rectangular region representing all possible outcomes. The rectangle has width π and height D, for an area of πD. |
|
For D < L,
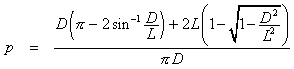
Back to Whistler Alley Mathematics