Tangent to a Conic

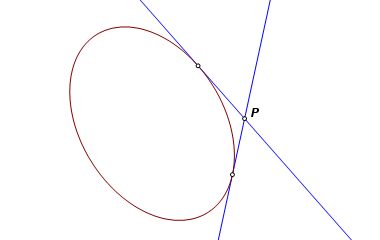
Given a conic section and an arbitrary point on its exterior, construct the lines through the point and tangent to the given curve.

This construction is presented in a single page addressing all applicable conics. Interestingly, the same construction applies in all cases. There can be no tangent lines to degenerate conics (except, perhaps, the trivial case of a point). That leaves ellipses, hyperbolas, parabolas, and circles. If the given point is on the exterior (convex side), there are always two solutions. If it is on the curve itself, there is one. It the point is on the interior (concave side), there are zero solutions. These constructions apply only to the exterior case.

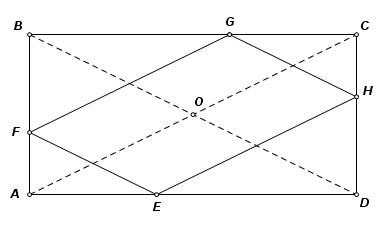
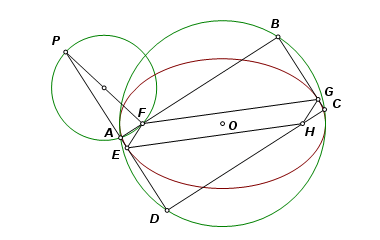
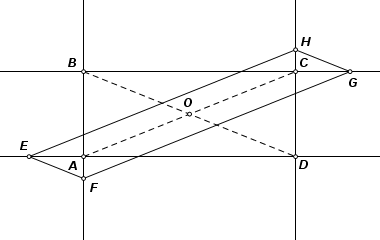
Consider rectangle ABCD and parallelogram EFGH inscribed in such a way that each side is parallel to one of the rectangle diagonals. The sum of adjacent sides of the parallelogram is equal to the diagonal length of the rectangle. Adjacent sides of EFGH intersect a side of the rectangle at equal angles.

Let O be the midpoint of line segment FH. Construct circle O with diameter greater than FH. Point A is on the circle, and AF is produced to intersect the circle at B. Complete inscribed rectangle ABCD. By symmetry, point H must lie on CD.

Complete parallelogram EFGH as shown, with sides parallel to the diagonals of the rectangle. It has these properties:

EF + EH = circle diameter

∠FEA = ∠HED

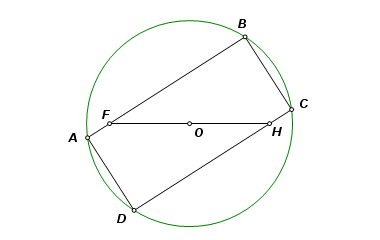
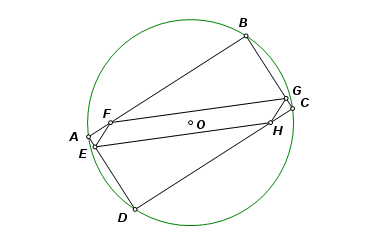
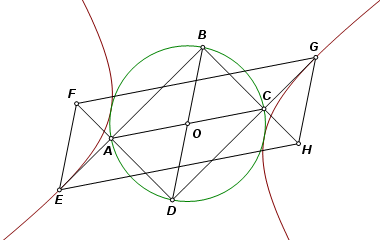
Let points F and H and the circle remain fixed, and let point A travel on the path of the circle. From the above properties, it may be concluded that the locus of E is an ellipse, line AD is tangent to the ellipse, and the major axis is a diameter of the circle.

Let P be a point on line AD. Angle PAF, being the exterior angle of a rectangle, is a right angle. Point A, therefore, lies on the circle with diameter PF. By construction, it also lies on circle O.

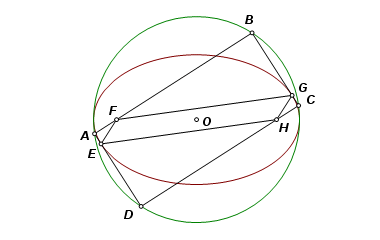
Here is one more useful property. Reflect an ellipse across a line of tangency. From the point of tangency the lines through the two foci intersect the line of tangency at equal angles. The same is true of the reflected image. As a result, the point of tangency lies on the lines joining each focus with the reflection of the other.

The relationships shown above provide the means to constuct the tangent lines. An ellipse was used in the illustrations, but it will be shown that the same construction applies to all curved conic sections. We begin here with the ellipse.

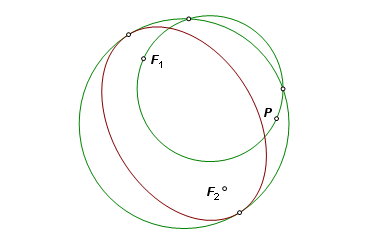
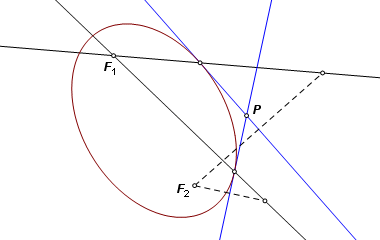
We are given an ellipse and point P on its exterior. Using methods described in ellipse parts, construct the center, the foci, and the major vertices.

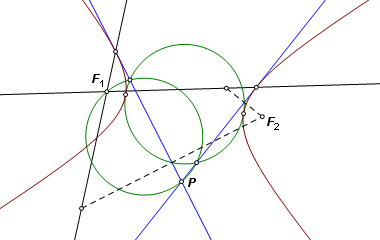
Construct the circle that shares the major diameter, and construct the circle having diameter PF₁, where F₁ is one of the foci. The circles will intersect at two points.

From point P draw a line through each of the intersections. These are the two tangent lines.

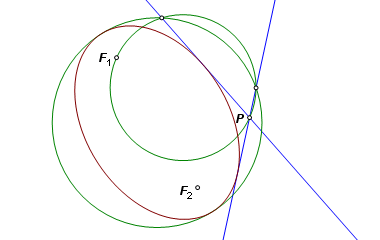
Reflect F₂ across each of the lines of tangency. From F₁ draw lines to each of the reflection points. These lines intersect the respective tangent lines at the points of tangency.

The completed construction.

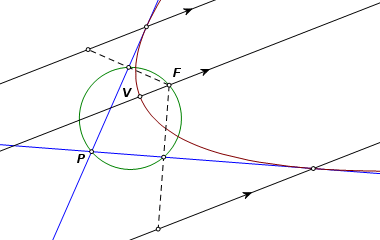
For the case of the hyperbola, a circle is again constructed between the vertices, but this time the foci fall outside of the circle. This changes a few of the underlying relationships, but the resulting construction is still the same.

Recall the relationships that were shown for the parallelogram inscribed in the rectangle. This time the vertices of the parallelogram are attached to the produced sides of the rectangle. The sides are again parallel to the diagonals of the rectangle.

Adjacent sides of the parallelogram still intersect a rectangle side at equal angles. This time, however, the difference of adjacent parallelogram sides is equal to the diagonal length of the rectangle.

This construction is equivalent to the one that was used for the ellipse, the only difference being that foci F and H are now on the exterior of the circle.

This time, because of the relationships above, as point A travels the circle, the locus of E is a hyperbola. Produced side AB is again tangent to the curve, and again, ∠BAF is a right angle.

What this means is that we can use the same construction for tangents to a hyperbola. There are also corresponding reflection properties facilitating construction of the points of tangency.

The completed construction.

For the parabola, there is no rectangle and parallelogram corresponding to those used above. The tangent constructions were identical for the ellipse and hyperbola, and the parabola is a limiting case of both of those curves, which suggests that we can use the same construction again. One sticking point is the fact that a parabola has only one vertex, so there is no circle having a diameter defined by the two vertices. Or is there?

Begin with an ellipse and construct a circle on its major diameter. Hold one vertex and the corresponding focus fixed. Let the other vertex be sent on a journey along the major axis. As it approaches a point at infinity, the ellipse approaches a parabola, and the circle flattens into a line. The same thing happens when one vertex of a hyperbola is sent down the transverse axis.

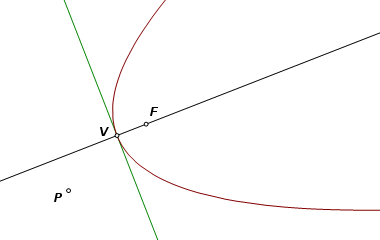
Begin with a parabola and a point P on the convex side of the curve.

Construct the vertex, focus, and axis of a parabola. Through the vertex construct a line perpendicular to the axis. This line is the limiting case of the circle that was used on the ellipse and hyperbola.

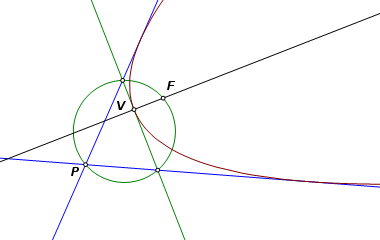
Construct the circle with diameter PF. From P construct lines through the two points of intersection. These are the lines of tangency.

Reflect the focus across both of the tangents. We would like to draw lines from these reflection images to the other focus, but there is no other focus.

We no longer have the second focus, but we do know what direction it went. It was traveling on the axis. Through each reflection point, construct a line parallel to the axis. They intersect the tangent lines at the points of tangency.

The completed construction.

Anyone following this is probably well familiar with the construction of tangents to a circle. It is shown here in order to complete the set, but also to show that the same construction is still in play.

Where are the vertices of a circle? The vertices of any conic are the points where the curve is intersected by its line of symmetry. But any line through the center of a circle is a line of symmetry. Corresponding vertices then are any two diametrically opposite points on the circle. Construct the circle between two such vertices and we simply get the same circle again. A circle may be imagined as an ellipse in which the foci have come together to a single point at the center.

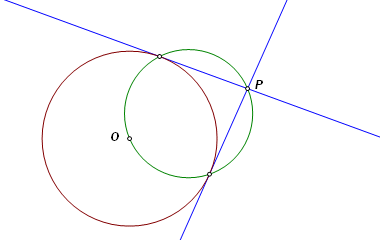
The given circle has center O and the given point is P. A circle is constructed with diameter OP. The intersection points again give direction to the tangents. This time there is no need to reflect a focus across the tangents to find the points of tangency. The intersections themselves are the points of tangency.

Back to Conic Constructions

Back to Whistler Alley Mathematics