Parallel Tangent

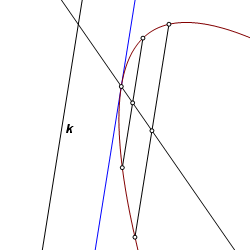
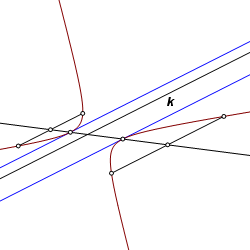
Construct a line tangent to a conic and parallel to a given line.

An axis of orthogonal or oblique symmetry intersects the curve at a vertex. The axis defines the abscissa direction, and a tangent line at the vertex point may be used to define the ordinate direction. Having done so, any chord in the ordinate direction is bisected by the axis. To effect the construction, we simply go thought this procedure in a different order. Construct the chords first, then the axis, and finally the tangent lines.

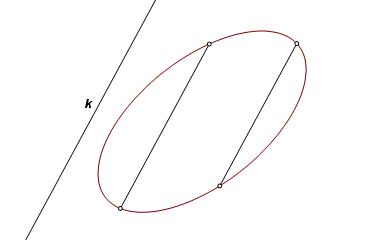
Using an ellipse in this example, let k be the given line. Construct two chords parallel to line k.

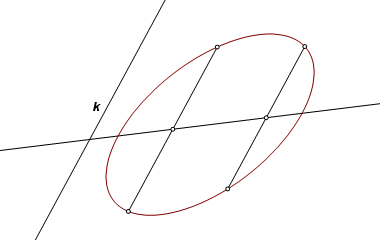
Construct the line through the midpoints of the chords. This is the axis of oblique (perhaps) symmetry corresponding to the two chords.

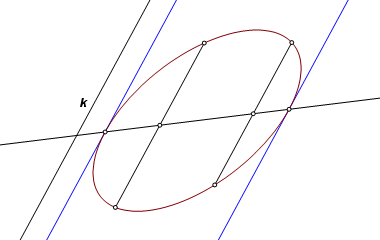
The axis intersects the curve at the vertices. Through these points construct lines parallel to k. These are the required tangent lines.

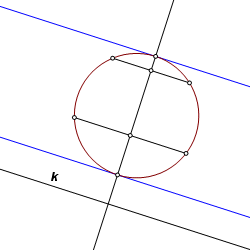
The same construction is applicable to all curved conics, and it fails only when there is no solution. In cases of an ellipse or a circle, there are always two tangents. For a parabola, there is one solution, unless the given line is parallel to the axis direction, in which case there are no solutions. For a hyperbola, there are many cases with no solutions. Otherwise there are two.

Back to Conic Constructions

Back to Whistler Alley Mathematics