Parabola Parts

Given a parabola only, construct its axis, vertex, focus, and directrix.

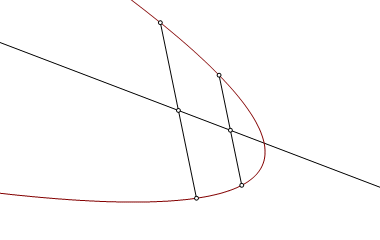
Begin by constructing an arbitrary chord on the parabola, and construct the midpoint of that chord.

Construct a second chord parallel to the first, and construct its midpoint. The line through the midpoints is an axis of oblique symmetry. It is parallel to the axis of orthogonal symmetry.

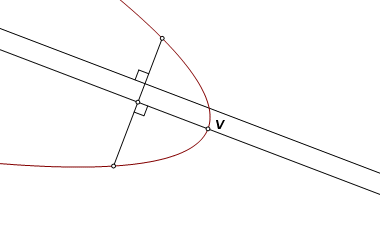
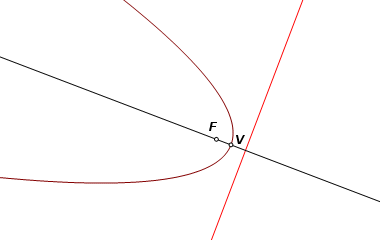
Construct a chord perpendicular to the axis of oblique symmetry. The perpendicular bisector of the chord is the axis of orthogonal symmetry, and that axis intersects the parabola at the vertex, V.

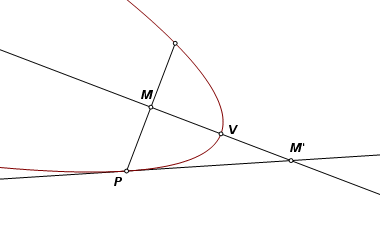
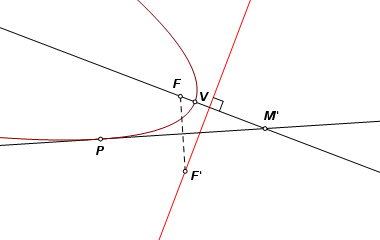
Let P be one endpoint of the orthogonal chord, and let M be the midpoint. Let M′ be the image of M reflected through V. That makes line PM′ tangent to the parabola at P.

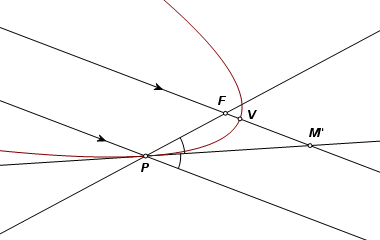
In an ellipse or a hyperbola, a tangent line bisects the angle formed by the lines joining the point of tangency to the two foci. A parabola is a limiting case of either of these curves, where one focus has been sent to a point at infinity in the direction of the axis. We cannot plot that missing focus, but we do know in what direction it lies. With that knowledge we can construct the other.

Through point P, construct a line parallel to the axis. Reflect that line across the tangent PM′. The reflected image intersects the axis at the focus, F.

The reflection of a parabola’s focus across a line of tangency must always fall on the directrix. Construct point F′, the reflection of point F in line PM′. Through F′ construct the line perpendicular to the axis. This is the directrix.

The completed construction.

Back to Conic Constructions

Back to Whistler Alley Mathematics