Parabola Given the focus and Two Tangents

Given the focus of a parabola and two lines tangent to the curve, construct the parabola.

This may be considered a special case of another construction that requires a focus and three tangent lines. If ellipses and hyperbolas require three tangent lines, how can the parabola be done with only two? The knowledge that the curve is a parabola satisfies the degree of uncertainty that would require a third tangent line otherwise. By similar reasoning, if we knew it was a circle, we could make do with only one tangent line.

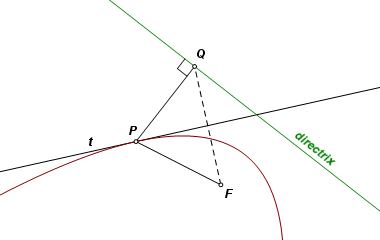
Suppose that the parabola is already known. Here it is, with its focus F and its directrix. Some simple properties of the parabola are in play. Let P be a point on the curve, let Q be its orthogonal projection on the directrix, and let t be the tangent line at P. In that case, ∠FPQ is bisected by line t and PF = PQ. That means the Q must be the reflection image of F across t. If the focus is reflected across any line of tangency, its image must fall on the directrix.

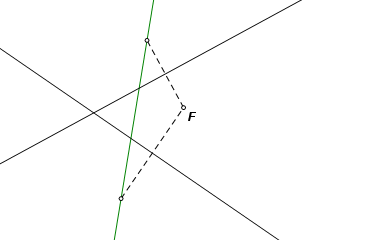
The construction:

Here we are given focus F and the two tangent lines. Begin by reflecting F across each of the lines. The two image points define the directrix.

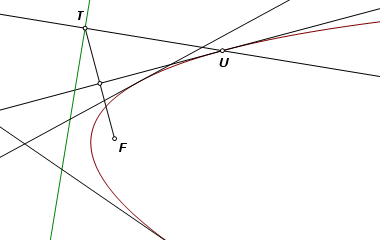
Let T be a traveling point on the directrix. Construct a line perpendicular to the directrix at T, and construct the perpendicular bisector of FT. These two lines intersect at point U, a point on the curve. The parabola is the locus of U as T travels along the directrix.

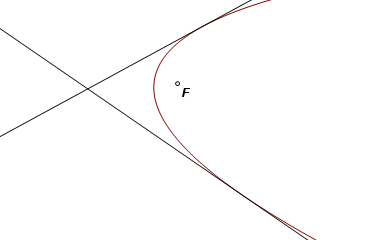
The completed construction.

Back to Conic Constructions

Back to Whistler Alley Mathematics