Focus and Three Tangents

Given one focus of a conic section and three lines tangent to the conic, construct the conic section.

This construction applies only to hyperbolas and ellipses (including circles). In the case of a parabola as a given condition, only two tangent lines are required. That case is addressed in a separate construction.

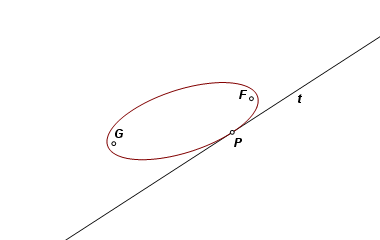
Suppose that the conic section is already known. Here is an ellipse with foci F and G, and line t tangent to the curve at P.

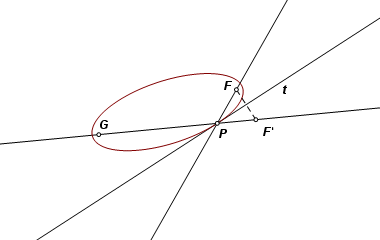
Line t, being a tangent, must be the external bisector of ∠FPG, and the sum of PF and PG must equal the major diameter of the ellipse.

Let F be reflected across t. Its image, F′, must fall on line PG, and PF = PF′. Therefore, GF′ is equal to the major diameter of the ellipse.

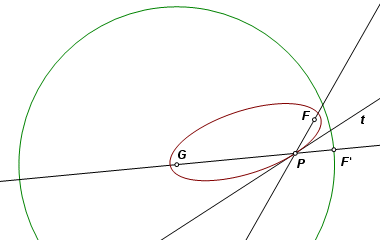
Now it follows that the image of F reflected across any line of tangency must fall on the circle centered on G and having radius equal to the major diameter of the ellipse.

Here is the equivalent relationship as applied to a hyperbola. In this case, tangent line t is the internal bisector of ∠FPG, and GF′ is the difference of PF and PG. The reflected images of F must now fall on the circle centered on G and having radius equal to the diameter on the transverse axis of the hyperbola.

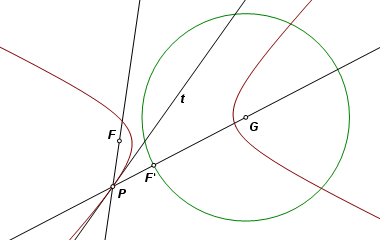
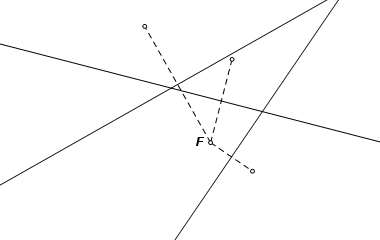
The construction:

Here we are given focus F and three tangent lines. Begin by refecting F across each of the lines.

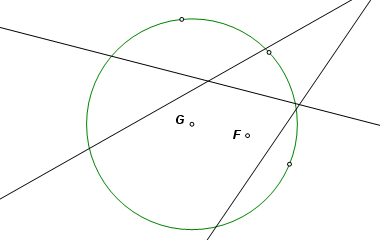
Construct the circle through the three reflection images, and construct point G, the center of that circle.

In the case of a parabola, the three reflection images would be collinear, which is one reason why that case was treated separately.

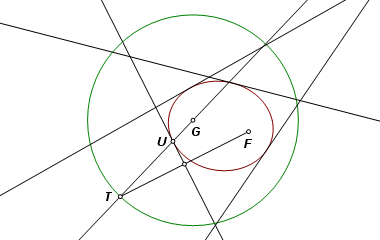
Now work backwards to construct a line of tangency. Point T is a traveling point on the circle. The line that reflects F to T is the perpendicular bisector of FT. That is a line of tangency, and it intersects GT at U, the point of tangency. The conic section is the locus of U as T travels its circular path. The solution in this example is an ellipse, but the same construction applies in the case of a hyperbola.

The completed construction.

If Java is enabled in your browser, drag point F to view other cases and their solutions.

Back to Conic Constructions

Back to Whistler Alley Mathematics