Ellipse Parts

Given an ellipse only, construct its major and minor axes, center, vertices, foci, and directrices.

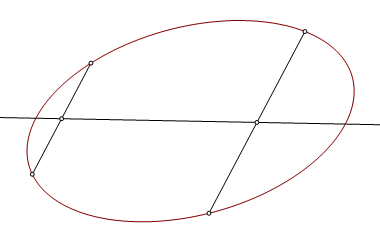
Begin by constructing a chord anywhere on the figure, and construct the midpoint of that chord.

Construct a second chord parallel to the first, and construct its midpoint. The line through the midpoints is an oblique axis of the ellipse.

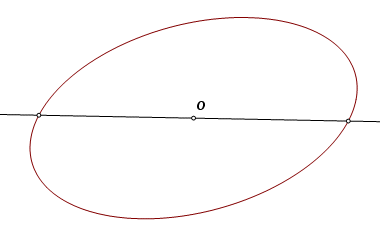
The intersections of the oblique axis and the ellipse are not vertices (not in the usual sense), but they do have this useful propertery. The midpoint, O, of the chord is the center of the ellipse.

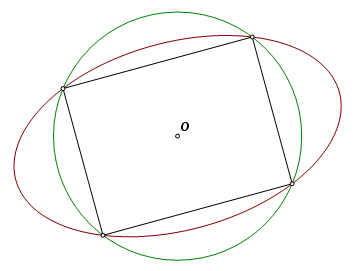
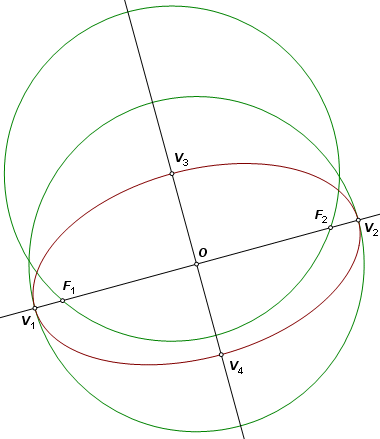
Construct a circle centered on point O and intersecting the ellipse at four points. These are the vertices of an inscribed rectangle.

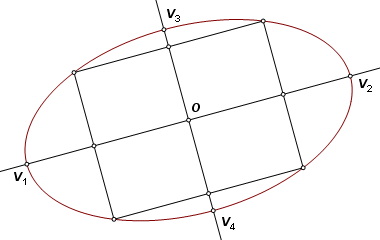
The rectangle and the ellipse have the same axes of symmetry. Construct the lines through the midpoints of opposite sides of the rectangle. These are the axes of orthogonal symmetry of the ellipse. They intersect the ellipse at the four vertices, here labeled V₁, V₂, V₃, and V₄.

From any point on the ellipse, the sum of the focus distances must be V₁V₂, the length of the major axis. Construct the circle with diameter V₁V₂. Translate it so that the image is centered on minor vertex V₃. Let it intersect the major axis at F₁ and F₂. These are the foci because they are on the major axis and satisfy these two conditions:

V₃F₁ + V₃F₂ = V₁V₂

V₃F₁ = V₃F₂

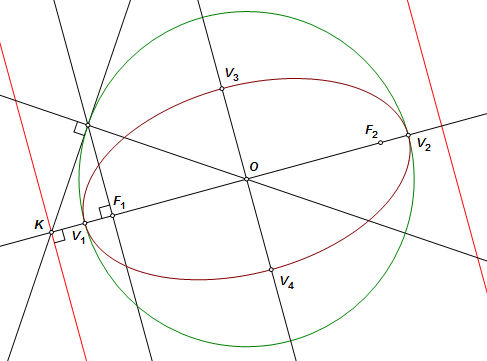
Let K be the point where the major axis intersects the directrix corresponding to focus F₁. Then KF₁ must divide V₁V₂ harmonically. Equivalently, K is the inverse of F₁ with respect to the circumcircle. To construct K, project F₁ perpendicular to the major axis onto the circle, then tangent to the circle onto the major axis. The directrix is then constructed through K perpendicular to the major axis, and the other directrix is its reflection across the minor axis.

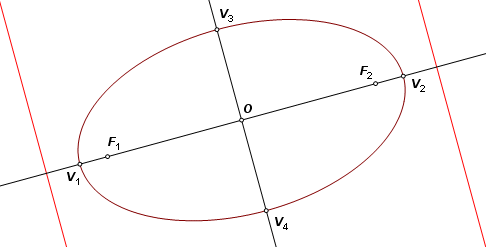
The completed construction.

Back to Conic Constructions

Back to Whistler Alley Mathematics