Theodolite Error

The trunnion axis is not perpendicular to the vertical axis.

When the scope is turning about the trunnion axis, the line of sight should sweep through a vertical plane. If the trunnion axis is not perpendicular to the vertical axis, then this plane will be deflected. On level ground, the error may be very small, but traversing up or down a steep hill will increase the error.

In this exaggerated illustration, the trunnion axis is listing to the right. The locus of the line of sight is a plane. It intersects the desired vertical plane on a horizontal line. Looking uphill, the line of sight is deflected to the right. Looking downhill, in misses to the left. Imagine having a steep uphill backsight. The reading on the horizontal scale would be to the left of the actual sight. Looking at a steep downhill foresight, the scale reading will be to the right of the sight direction. This results in an angle measurement (clockwise) that is too large.

In the formula below, δ is the clockwise horizontal deflection of the line of sight from the scale reading, φ is the true zenith angle, and α is the clockwise deflection of the trunnion axis from the perpendicular. As shown above, the line of sight must be projected onto the horizontal plane in order to measure the deflection error. Note that δ goes to zero and then changes sign as φ passes 90°.

Here is the best reason for reading both sides. When the scope is inverted, the line of sight still travels through an oblique plane, but now it is listing in the opposite direction. On the uphill backsight, the scale reading now misses to the right. On the downhill foresight, it misses to the left. The result of the inverted reading is an angle that is too small, compensating for the error in the direct reading.

The line of sight is not perpendicular to the trunnion axis.

Suppose now that the trunnion axis is perpendicular to the vertical axis, but the line of sight is not perpendicular to the trunnion axis. Again the images are exaggerated in order to make the point. This condition is not actually cause by a poorly mounted telescope. It is more likely a misalignment of the crosshair reticule inside the scope.

This time when the scope turns on the trunnion axis, the line of sight sweeps a cone rather than a plane. While the scope is in the direct position, the deflection is always in the same direction, but variable in magnitude. On steep ground, it even has a tendency to take care of itself, because the backsight and foresight may have close to the same deflection. The worst error occurs when one sight is much steeper than the other.

The vertical axis is not plumb.

Of the three horizontal errors, this one is, perhaps, the least significant and the easiest to correct. It is only a matter of leveling the instrument properly. Unfortunately though, this is one case in which the transiting capability of the theodolite does nothing to correct the error.

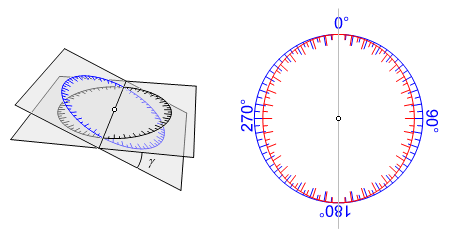
In this image, the black scale is level and shows the true direction, but the tilted blue scale is the one that is actually being read. There is a line of intersection running through the middle of both scales. This line of intersection is arbitrarily given a direction of 0° here, but it has no relationship to the direction in which the instrument is pointed. The error can be observed by projecting the true scale onto the plane of the instrument scale. The (red) projection is elliptical, and the scales coincide only when the line of sight is along or perpendicular to the line of intersection (0°, 90°, 180°, and 270°).

That is not where it ends. That simplified description assumes that the line of sight is level. Suppose that the instrument is pointed upward or downward. As the instrument turns, assuming a constant φ, the locus of the line of sight is a cone with a vertical axis. When the true scale is projected onto this cone, it is still true (the purple scale in the image). This scale in turn is projected onto the plane of the instrument scale. The result is a translation of the elliptical scale above, and it is true only when the line of sight is perpendicular to the line of intersection (90° and 270°).

The geometric transformation of the scale is not really so complicated, but the corresponding analytic formula is. This is no bother since the formula has no practical value anyway. Here δ is again the deflection of the line of sight from the scale reading and φ is the true zenith angle. The variable θ represents the true clockwise horizontal angle from the line of intersection of the two planes. When the instrument is pointed in the direction of the line of intersection, with the “vertical” axis listing to the right, then θ is 0°.

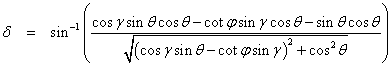
The condition described here is an issue of leveling, and transiting the instrument does nothing to compensate for it. Check the level vials frequently.

The vertical angle collimation is out of adjustment.

Theodolites measure vertical angles, usually from the zenith direction, sometimes from the horizon, rarely from the nadir. This difference affects nothing but the arithmetic. The vertical axis should point to the zenith, but for greater precision, theodolites have separate collimation systems so that the angle is referenced directly to the gravity vector. This system may use a leveling vial or a pendulum compensator, either of which can go out of adjustment.

A theodolite would make a very inefficient level (except for trig leveling, another topic), but it essentially carries a level in its housing. The leveling vial is equivalent to a tilting level, and the pendulum compensator does the work of an automatic level. The theodolite actually has one advantage over most levels. By inverting the telescope, the collimation can be checked from a single setup.

If a vertical angle is measured in both direct and inverted positions, then the sum of the observations should be 360°. The collimation error, ε, will either add to both observations or subtract from both, so it will show up in the sum of the two angles. In this picture, two observations are made on the same stationary target. The measured vertical angle is φ₁ in the direct position, and φ₂ in the inverted position. Find ε using the formula below, and subtract it from the direct observation to get the true vertical angle. In the illustration, both measured angles are too small, and ε is negative.

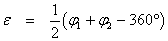
A few seconds, or even minutes, of error here makes no appreciable difference in horizontal distances, but it can play all havoc with elevations. Unlike the horizontal angle errors, this one is constant, which is to say, it is not affected by changes in the direction of the sight. That makes it a fairly simple matter to correct the angle without even adjusting the instrument. In fact, electronic instruments typically have an onboard routine that will measure and correct the vertical angle error. Push a few buttons, sight a target in both positions, and have the instrument store the correction. The procedure takes only a couple of minutes, so it can be done at the beginning of each work day.