The Repeating Horizontal Scale

The repeating horizontal scale is yet another way of coping with limitations in manufacturing and reading a precise arc scale. Not long ago, the pointing precision of a theodolite was considerably better than the scale precision, even with the help of the vernier scale. It might be possible to turn an instrument to within five seconds of a target consistently, but what good is that if the instrument’s least count is thirty seconds?

To understand the solution, consider this analogy. Suppose the objective were to measure the thickness of a single sheet of paper. Measure the height of 500 sheets and divide the measurement by 500. Even under the worst conditions the error in the measurement would be less than 5 mm. Divide that by 500, and the error in the answer is less than 0.01 mm. The result is not actually the measurement of one sheet, but rather the mean thickness of 500 sheets, which would probably be a more useful figure anyway.

The repeating theodolite uses the same principle. It places several angle observations end-to-end on the same scale. This way the final reading can be divided by the number of observations. The procedure is called wrapping a set of angles. This expression may have come about because of the way the angles are wrapped around the scale like a thread on a spool. It might also be a curruption of the word repeating. Some people pronounce it repping.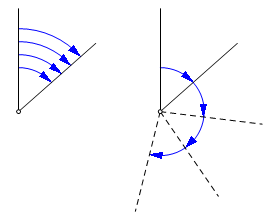

Here is how it works. The theodolite has two horizontal motions, and upper and a lower. While the instrument is in use, no more than one of the scales is free to move at any one time. When only the upper motion is released, the telescope moves and the scale is stationary, so moving the scope changes the angle reading. When only the lower motion is released, the scope and the scale move together, and changing direction does not change the scale reading.

On the initial backsight, a reading of 0° is loaded on the scale. The instrument is then turned on the upper motion to the foresight and the scale reading is recorded. Next, the lower motion is released and the scope is again turned to the backsight with the measured angle still on the scale. The upper motion is released and the scale advances as the scope is turned again to the foresight. At this time, the scale reading is two times the angle. The steps are repeated for any number of repetitions. There should be an even number, half direct and half inverted.

The final reading is the sum of the measured angles. The instrument may have gone all the way around the scale one or more times, so multiples of 360° are added to the final reading as required. The sum is then divided by the number of turns. Only two of the scale readings actually affect the outcome. They are on the first (0°) and the last observations. The first foresight confirms the degree reading and serves as a redundancy check, but it has no influence on the precision.

As an example, consider a transit with a least count of one minute. Assume perfect instrument calibration and zero human error in pointing and in reading the scale. That still leaves as much as 30" of rounding error every time the scale is read. In this example, the scale reading is in error by -22":

Four angles are turned, so the scale has been advanced by the true angle four times. The scale is then rounded to the nearest minute again.

The Downsides

• One advantage of wrapping is that there are fewer scale readings and recordings. Typically there are only three readings: the initial zero setting, the first foresight, and the final foresight. If there is an outlying angle measurement, it might very well go undetected. Blunders can slip through more easily.

• Sometimes there is a problem on one observation. Someone kicks a leg or turns the wrong knob. In that case, the entire set has to be run again from the beginning. This is particularly a concern when using a large number of observations with an instrument operator who is lacking in experience or grace.

• It is not possible to have more than one foresight in a single set. Turning multiple sets requires more time, but the precision argument is still valid.

Back to The Geometry of Surveying