Questionable Practices

Wrapping Angles

This practice makes effective use of a repeating theodolite. The lower scale is repeatedly carried to the backsight. As a result, there are only two scale reading errors, and they are spread across all of the observations. This serves to diminish the error. The effectiveness of the technique is explained on a separate page. My beef is not with the theory of wrapping angles, but rather with its inappropriate application.

Remember why this procedure was developed. At one time, the scale reading was the greatest human error associated with turning an angle, because the scale had to be read directly. This is no longer the case. Optical micrometers can split an angle much more finely, and electronic micrometers even do the reading for you. With the better instruments, the scale reading may actually have greater precision than the instrument pointing.

Do you even have a repeating theodolite? On a second turn, I have seen gunners turn a directional theodolite to a backsight and then load a recorded reading into the scale. Often directional theodolites do not even have a fine adjustment for the scale setting, so this is like tuning a violin with a pipe wrench. Also, this method requires a scale reading on each observation, so every advantage of wrapping is lost. The end result is more time, more calculations, and less precision.

There have been true repeating electronic theodolites on the market, with separate upper and lower motions, but most electronic theodolites are directional. Electronic directional theodolites usually offer some sort of routine that will simulate a repeater. A foresight reading is carried to the backsight, but the scale itself does not move at all. In this case, no extra observation time is spent and only a little effort is wasted, but no precision is gained. I was once required to wrap angles on all work done for the local municipality, this because of some outdated engineering standards. We filled (or rather, simulated) the requirements with an electronic total station.

For traverse angles, wrapping is no great bother, but for observations with multiple foresights, it can require considerably more time. For each additional foresight, there are two superfluous backsight observations and one more scale setting. This becomes especially wasteful in stake-out work.

Unadjusted Control

One school of thought holds that if a closure is within tolerance, then there is no need for adjustment, because the coordinates (horizontal and/or elevation) have an acceptable degree of uncertainty. That is fine for location work, but what becomes of the control that is to be used later? My own position is that it is not acceptable to have a significant discrepancy between adjacent control points. That point is illustrated here with two level circuits, both of them based on experience. Similar problems arise in horizontal control.

The first circuit is a loop beginning at a benchmark. Several temporary benchmarks are established along the way, the last one, TBM5, being set just across the street from the controlling benchmark. The error of closure is an acceptable -0.04 feet over the two-mile loop. If no adjustment is made, then the elevation of TBM5 depends entirely on the two miles of leveling while the final 50-foot run to the benchmark is being disregarded. The end result is a 0.04-foot discrepancy between two monuments that are observable from the same instrument position.

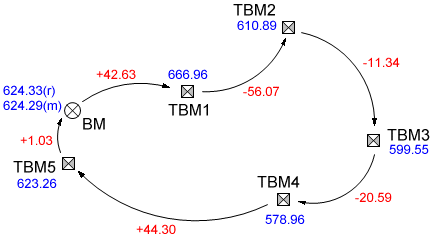
The second circuit retraces its own path, hitting the same TBMs both forward and back. Again, there is no adjustment. This time the result is conflicting elevations on the same monuments.

Reading Angles on One Face

The Theodolite Error section has repeated references to systematic errors that can be turned against themselves simply by reading angles on both faces of the instrument. Unable to convince a superior of this fact, I once had to forego the practice under certain conditions that must have greatly exacerbated the problem.

We were traversing along the boundary of a deep, narrow parcel. The terrain was very steep. Starting from the frontage road, we worked our way downhill maybe 1500 feet, crossed the parcel, and came up on the other side. Now imagine the inevitable error from a trunnion axis that is not quite level. Working down the hill, every angle error would be in the same direction. Coming back up, the error would be thrown in the opposite direction. There were about the same number of setups in both directions, so the opposing errors gave us a fairly good angle and position closure, good enough to encourage self-deception.

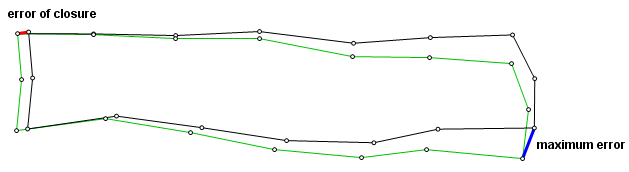
The sketch above illustrates and exaggerates the situation. The black courses show the traverse according to the observations. The green courses are the actual route. The traverse begins at the northwest corner. The error of closure (in red) is acceptable, but the maximum positional error (blue) is in the southeast, and it is far worse. Rather than eliminating error, we were using a procedure that concealed it.

Radial vs. Gridline Staking

Points to be staked at a construction site often fall in a line or on some sort of rectangular grid. It could be a line of building corners, a row of columns, or stations along a centerline. Until recently, there was little choice in how to go about it. From a control point, a point was staked on the alignment. The instrument was then moved to that point, and stakes were set in a line. When fast field computers with coordinate storage capabilities became available, it became practical to stake each of the points directly from the control point. The instrument did not need to be aligned with the grid at all.

With two methods now available, their advocates began to fall into two different camps. The rectangular stakers, usually the old guard, insisted that the traditional method was less prone to blunders, and that their stakes lined up better. The radial stakers argued mostly from a position of efficiency. The argument about stake alignment is hard to dispute, but one point that I wish to make here is that alignment should not be confused with positional accuracy.

All measurements are in error. When we set out a point, we turn an angle and measure a distance, both of which are in error. The distance error is along the line of sight. The angular error results in a positional error nearly perpendicular to the line of sight. This is the departure error. On a short sight typical of a confined construction site, and using modern, properly calibrated instruments, the departure error is considerably less than the distance error. For a given level of confidence, a staked point falls within an ellipse, the major axis of which is along the line of sight.

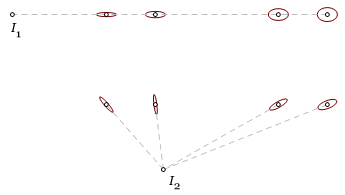Here is an error analysis of the two methods in comparison. First, four points are staked in a row from instrument position I₁. There is a certain confidence (say 0.95) that the points fall within their respective ellipses. Since the major axes are aligned, the points will be very close to alignment. On the right, the same four points are staked radially from point I₂. This time some of the major ellipse axes cross the gridline at steep angles, so we cannot expect such a good alignment. However, the positional accuracy of the radial method is at least as good.

There are some other rectangular downsides that should be discussed here. The above-mentioned alignment applies in only one direction. On a building site, the staked points fall on gridline intersections. After staking them along parallel lines, the alignment in the perpendicular direction will be disappointing. Another issue is that, with rectangular staking, the instrument is usually at least one more setup removed from the control.

Refusal to Round a Reading

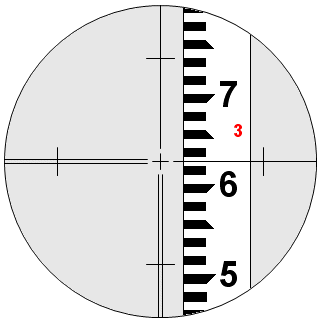
This is a habit that can really put a drag on a field party. The rod reading shown here falls midway between two graduation marks. Is it 3.62 or is it 3.63? I have worked over and under several instrument operators who simply refuse to commit. On a backsight, they may shake up the instrument and read again. If it is a foresight, they might even call out to the rodman and tell him to hit the turning point. When I was recording, one fellow used to give me both readings and then qualify it by saying, “whichever you prefer.”

We do round numbers, and it is best to round to the nearest mark. In this case, it is not possible to tell which is nearest. Look at it this way. If the crosshair were at 3.624, we would be happy to call it 3.62 and cast four thousandths to the wind. So why should we balk at five thousandths? Just read the rod and keep the work moving.

EDM vs. Chaining

I once worked with a firm that had a standing policy that all distances less than 300 feet must be chained. The reasoning here was that in that range, a chain is more accurate than an electronic distance measurement (EDM). This seemed reasonable to me, but in practice, it often became very inconvenient, time-consuming, and decidedly inaccurate. Somehow, without even noticing it myself, I changed the limit to 200 feet, which was the length of my chain. No one said anything.

On closer consideration, I have come to believe that the 300-foot limit, though not arbitrary, was overly-simplified. The chain prevails at short distances under laboratory conditions. In practice, a field party must contend with obstructions and crosswinds, both of which affect chaining more severely than they affect EDM measurements. Temperature corrections are suspect because on a sunny day, the temperature of the chain can be much higher than the measured temperature of the air. Another matter, regrettably, is the declined chaining skill of the modern, pampered surveyor.

The words above are true, but they are also the words of someone trying to ease his own conscience. Chaining can be very inconvenient, and that is the real driving reason. A third party member is now a luxury, and the fourth member must surely be extinct, so who has enough time and enough hands?

And what of that supposed increase in error? What are the consequences? Distance error, unlike angular error, does not lead to greater problems down the road. One hundredth here means one hundredth at the closing point. Also, with few exceptions, the short distances that would be chained are on side shots, not traverse legs, so the control is not compromised.

Divining Rods as Locators

Oh, good grief.

Point-on-Line

As with some of the other topics on this page, the point-on-line is a good practice that is often used improperly or for the wrong reasons. If it is necessary to move a theodolite a short distance, for instance, to see around an obstacle, a point is set in line with an adjacent control point, the instrument is moved up to it, and the same backsight is used again. This eliminates the need to use a short backsight. There is no scale reading, and nearly zero angular error. Since the backsight azimuth is the same, it even makes the calculations a bit simpler.

The disagreement comes when the point-on-line is embraced as some sort of panacea, never an error, never a worry. Points might be set with impunity at any distance as long as they fall on a control line. In the past, I have been instructed to set points-on-line at distances approaching 2000 feet, even in poor visibility. That is simply another traverse leg, and not a very good one at that, because the angle (0°) is staked rather than measured. See more on staked traverses below.

Staking a Traverse

For various reasons, survey parties often place (rather, attempt to place) traverse stations at specific locations, such as centerline stations or boundary corners. This is not necessarily a bad thing, but it requires certain sacrifices that should be considered.

As a general rule, it is possible to measure an angle and distance with greater precision than to set a mark at some predetermined angle and distance. The former method involves a single observer with stationary targets, and it is a simple matter to repeat the measurement. Staking, however, requires coordination and communication between two or more people. Precision aside, staking has some other disadvantages. The traverse point may fall in a difficult position, such as a ditch slope or a traffic lane. If the point is being used for something, such as construction work or monumentation, a survey party may see all of their control destroyed in a single day.

One benefit of staking a traverse is that the staked points are checked when the traverse is closed. Otherwise, some other redundant check is needed on the side shots. One persuasive argument for traverse staking is now getting rather dated. It simplified calculations. Someone would work out the whole traverse, and the field party would stake the specified courses. Modern field computers make those calculations superfluous. A party chief can easily coordinate points on the fly.

In what was, for me, a rather frustrating experience, I once worked with an outfit that insisted on using rectilinear staking on all of their traverses. Every sight was in a cardinal direction: north, south, east, or west. Every angle was a multiple of 90°. We were on flat, bare terrain, which made this possible, but by no means practical. Although this happened during an era when a few coordinate geometry calculations were no problem, the prevalent opinion was that the method was more precise. In fact, the instrument measured 90° with no greater precision than 91°. All of the traverse points were staked, and there were nearly twice as many traverse points as needed.

Rocking the Rod

This one is on perfectly firm geometric footing. A turning point is a point, and a level instrument defines a level plane. The perpendicular distance from the point to the plane is less than the distance to any other point in the plane. A rodman sways the rod to and fro, and the instument operator notes the lowest reading. Nothing could go wrong.

Now do it while peering at a dim flashlight glow in an arctic night. The gusts are tossing your head like a windsock. The moisture from you breath is crystalizing on the lens and on your eyelashes. The rod comes into focus briefly, but it is a moving target, so you wait to see it again, and again.

Acquire a rod bubble and learn how to keep it in proper adjustment.

Unwarranted Faith in Instruments and Software

Surveying instruments, like everything else in our lives, have become more complex. At the same time, they have become more opaque. Looking at a 100-year-old instrument, it is fairly easy to figure out the function of most of its many moving parts. Try that with a modern total station. The only things visible are two knobs, an eyepiece, and any number of buttons. Our understanding of the instrument’s guts sometimes verges on superstition.

Sad to say, these misunderstandings are often encouraged by the people who sell them. I do not intend to start some long gripe about salespeople. I like most of them, and they take more heat than they deserve. However, they often do not fully understand the mechanics of their instruments or the practice of surveying. Consequently, their claims and advice must be weighed against experience and geometric fact.

Surely the most egregious false claim I have heard came from a dealer who told me that his instrument had such advanced internal compensators that there was no longer any reason to invert the telescope. In fact, said he, after turning an angle on one face, it would be a pointless exercise even to check the backsight. This claim was not only wrong; it was preposterous. After proving that fact geometrically, I confirmed it in an interview with a technician employed by the manufacturer.

Software is far less dependable than the instruments. This is natural since a program can be edited every day without having much effect on the production line. There were a few times when, after acquiring a new system, I went into the office on a weekend, set up an instrument, scattered a few prisms around the room, and tried every function in the manual. I did not want to be learning the system in the field, with people waiting on me, but also I wanted to confirm that it was actually doing what it should be doing. Disappointments were frequent. I sent so many bug reports to one developer that it occurred to me that I was being used as an unpaid quality control consultant. After making the patches, they billed me for an upgrade.

Unrealistic and Unnecessary Accuracy Demands

Here are two questions that are not asked often enough: What level of accuracy can reasonably be expected? What level of accuracy is needed?

All measurements are in error. Unfortunately, some believe that all errors are blunders. Often unreasonable demands come from within a survey firm. An error of closure falls within tolerance, yet a scornful glare is cast upon the party, with especially intense reproval directed toward the gunner. Who screwed up? It is possible that this type-A supervisor haplessly stumbled into a flat closure during his youth and spent the rest of his career believing that flat closures were the norm.

Clients often are another source for these demands. This is why I once spent an afternoon checking positions on a row of mooring piles, using a supposed positional tolerance of 1/8 inch. My employers were only too pleased to take on such contracts. They were aware that we lacked the instruments and expertise to fill such requirements, but they also knew that there was no one else available who could follow the specs to the letter. After I finished, those same piles surely endured a short, violent existence, tortured by winter gails and slammed by ships the size of shopping centers.